Simulazione di Algoritmi Quantistici usando lo strumento Q#
DICHIARAZIONE DI ORIGINALITÀ
Dichiaro di essere responsabile del contenuto dell’elaborato che presento al fine del conseguimento del titolo, di non avere plagiato in tutto o in parte il lavoro prodotto da altri e di aver citato le fonti originali in modo congruente alle normative vigenti in materia di plagio e di diritto d’autore. Sono inoltre consapevole che nel caso la mia dichiarazione risultasse mendace, potrei incorrere nelle sanzioni previste dalla legge e la mia ammissione alla prova finale potrebbe essere negata.
\(\pagebreak\)
Introduzione
Lo sviluppo di software quantistici si è confermato come un’area di grande interesse negli ultimi decenni, offrendo grandi possibilità di superare i limiti computazionali attualmente raggiunti in diverse aree di ricerca. È possibile che in futuro algoritmi quantistici possano sostituire controparti classiche in diverse applicazioni:
- crittografia;
- problemi di ricerca, l’algoritmo di Grover in questo campo è quadraticamente più veloce del analogo classico;
- utilizzo di computer quantistici per la simulazione di sistemi quantistici;
- machine learning;
- computazione biologica;
- chimica generativa.
Ovviamente il calcolo classico non verrà abbandonato, l’approccio classico e quello quantistico differiscono nelle loro forze e debolezze. Mentre gli attuali computer diventano sempre più veloci e le tecniche industriali permettono miniaturizzazioni sempre maggiori gli hardware quantistici rimangono estremamente complicati da costruire e distribuire. Il modo attualmente più congeniale di utilizzare questi hardware per effettuare testing di software rimane quello della condivisione di risorse attraverso le tecnologie di cloud computing.
Ma questo non significa che non sia possibile o non sia utile studiare i problemi e le soluzioni algoritmiche che il calcolo quantistico offre a livello teorico e di sviluppo software. È importante sottolineare che ci aspettiamo che i computer quantistici e le risorse di cui dispongono scalino diversamente nel contesto di alcune classi di problemi da risolvere, in particolare permettendo per i problemi giusti, più adatti, di superare di gran lunga la performance dei migliori algoritmi classici. Questo perché l’approccio algoritmico permesso da questa tecnologia è profondamente diverso da quello classico e porta a miglioramenti importanti in termini di complessità computazionale. D’altra parte non ci si deve aspettare che questa sia una soluzione perfetta, ci sono problemi che rimarranno difficili da risolvere nonostante le nuove possibilità della computazione quantistica.
Per molto tempo l’approccio a questo campo è rimasto accessibile solo a matematici e fisici con le conoscenze specifiche necessarie a comprendere appieno la meccanica quantistica e le sue sfumature tecniche.
Questo sta cambiando velocemente negli ultimi anni da quando l’industria ha cominciato a sviluppare strumenti e piattaforme che permettano a nuovi sviluppatori di interagire e imparare in quest’ambito astraendo dalla maggior parte della complessità della teoria matematica alla base di questo modello.
Definizione di un Computer Quantistico
Per prima cosa definiamo un computer come uno strumento che prendendo dei dati in input esegue delle operazioni su questi dati.
I computer che conosciamo e utilizziamo attualmente possono e sono definiti nei confini teorici della fisica classica, ovvero attraverso le leggi di Newton e l’elettromagnetismo.
Data questa definizione è semplice definire un computer quantistico come uno strumento che prendendo dei dati in input esegue delle operazioni su questi dati con processi descrivibili solo utilizzando i concetti della fisica quantistica.
Detto questo la differenza tra un computer classico e un computer quantistico è la stessa che esiste tra la fisica classica e quella quantistica. La principale differenza è la scala su cui operano in termini di dimensioni e energia.
I calcolatori quantistici sono in ogni caso controllati tramite interfacce e strumenti classici con cui è più semplice interagire e tramite cui i dati sono riconvertiti in dati di tipo classico utilizzabili dalle CPU che comunemente utilizziamo.
In altre parole un computer quantistico differisce da uno classico nella sua capacità di non sottostare agli stessi limiti di complessità temporale nella risoluzione di problemi computazionali. Importante quando serve risolvere problemi complessi per cui non sono accettabili semplificazioni e ci si avvicina sempre di più ai limiti fisici nelle architetture hardware classiche. In questi casi infatti invece che creare supercomputer sempre più potenti può essere interessante un cambio di approccio, ritrovabile nel quantum computing.
Limiti Hardware
Attualmente i software sviluppati per hardware quantistici possono essere eseguiti su simulatori, sempre software, oppure sfruttando reali macchine quantistiche in remoto. Questo è necessario in quanto i requisiti e limiti tecnici della costruzione di un calcolatore quantistico sono estremamente complessi e richiedono ambienti fisici attualmente incompatibili con un utilizzo desktop. Questi limiti sono in particolare l’estrema sensibilità dei registri all’interno di un computer simile alle interferenze esterne, per ovviare a problemi di interferenza è necessario mantenere l’hardware in temperature vicine allo zero termico (\(0\text{K}\) o \(-273.15^{\circ}\text{C}\)). Queste condizioni non sono ovviamente replicabili in un ambiente non strettamente controllato e isolato.

Figure 1: Architettura globale di un computer quantistico - tratto da articolo IEEE Explore Journal: https://ieeexplore.ieee.org/document/9274431
Dati questi limiti è facile dire che per molto tempo ancora questo tipo di hardware sarà limitato a un utilizzo da remoto tramite architetture cloud, molte aziende private in questi anni hanno sviluppato soluzioni in questo senso.
Alcuni esempi sviluppati negli ultimi anni dai maggiori competitor sono IBM Q1, Google Quantum AI2, XANADU Quantum Cloud3 con la sua interfaccia python Strawberry Fields4 con supporto Tensor Flow integrato, Amazon Bracket5 offerto da AWS.
Queste sono solo le offerte più commercialmente rilevanti, sono tante le alternative che sarebbe possibile considerare.
I simulatori e le macchine reali condividono interfacce condivise che permettono lo sviluppo di software che abbia la possibilità di essere testato efficacemente.
Uno di questi simulatori é ad esempio qsim6, sviluppato dal team di Google Quantum AI questo simulatore permette di emulare circuiti quantistici in modo efficace fino a 20 qubit interfacciandosi con il framework Cirq7.
Utilizzi della tecnologia
I computer quantistici offrono nuove possibilità nella risoluzione di diverse classi di problemi, la ricerca in questo campo ha trovato alcuni esempi di algoritmi che utilizzando le proprietà particolari di questo approccio per sviluppare un vantaggio nei confronti dell’approccio classico.
Ad esempio:
- L'algoritmo di Grover effettua una ricerca in una lista di \(N\) elementi in tempo \(O(\sqrt{N})\).
- L'algoritmo di Shor fattorizza velocemente grandi numeri, in particolare permette di fattorizzare con un grado di errore arbitrariamente piccolo e un numero polinomiale di passi rispetto alla lunghezza in bit dell’input.
- L'algoritmo di Deutsch-Jozsa verifica se una funzione è costante o bilanciata in tempo costante \(O(1)\).
- L'algoritmo di Simon, ispirazione per il sopraccitato algoritmo di Shor, risolve in tempo esponenzialmente più veloce rispetto all’approccio classico il problema di determinare se una data funzione \(f\) blackbox sia uno-a-uno o due-a-uno.

Figure 2: Relazioni tra le classi di complessità, BQP indica tempo polinomiale quantistico con errore limitato
In aggiunta ai problemi di cui sopra, la cui soluzione è legata a un algoritmo in particolare, sono state trovate applicazioni per i computer quantistici in diversi altri ambiti:
- La stima di una somma di Gauss, un tipo di somma esponenziale, con precisione polinomiale e in tempo polinomiale contro il tempo esponenziale degli algoritmi classici.
- La valutazioni di formule booleane complesse può essere velocizzata tramite un approccio quantistico.
- Questi computer permettono di simulare sistemi quantistici permettendone uno studio più approfondito.
- La generazioni di numeri casuali è un’importante componente della crittologia e utilizzando tecniche quantistiche è possibile generarne che siano davvero casuali e non più pseudo-casuali come necessario in computer classici.
Questi sono risultati importanti e in particolare l’algoritmo di Shor pone dei dubbi sulla sicurezza degli attuali protocolli crittografici che si basano sulla difficoltà computazionale della fattorizzazione di grandi numeri interi. Se tale algoritmo fosse facilmente eseguibile significherebbe che un attaccante potrebbe facilmente violare questi protocolli di sicurezza correntemente alla base della comunicazione via Internet.
Rimane difficile trovare possibili algoritmi quantistici che diano un vantaggio computazionale nel campo dell’apprendimento automatico dove è fondamentale l’accesso casuale a una grande quantità di dati.
In generale è più probabile che un problema che abbia una piccola mole di dati in entrata e in uscita ma una grande quantità di manipolazioni per arrivare all’output sia un buon candidato per l’utilizzo di computer quantistici.
\(\pagebreak\)
Ambiente
Per lo sviluppo di software quantistici sono disponibili diversi ambienti e framework, tra i più conosciuti troviamo Microsoft Azure con il proprio Quantum Development Kit (QDK) o l’ambiente di sviluppo di IBM Qiskit.
Altri Software Development Kit che possono essere utilizzati per eseguire circuiti quantistici su prototipi di device quantistici o simulatori sono:
- Ocean
- ProjectQ
- Forest
- t|ket>
- Strawberry Fields
- PennyLane
Molti di questi progetti sono open source e sviluppati sulla base di Python.
Per questo lavoro abbiamo utilizzato gli strumenti offerti da Microsoft per l’ottima documentazione consultabile sulle loro pagine web e in quanto questo strumento era utilizzato dalla nostra fonte principale Learn Quantum Computing with Python and Q#.8
Nella documentazione ufficiale di Microsoft Azure è presente una guida9 all’installazione dell’ambiente di programmazione Q# di cui qui riportiamo dei passaggi.
Il lavoro per questa tesi è stato fatto in un ambiente Linux, il processo di installazione è del tutto equivalente nel caso si utilizzasse Windows utilizzando la powershell e conda o pip.
L’ambiente di esecuzione Q# può essere configurato sul editor Visual Studio Code tramite l’add-on proprietario Microsoft Quantum Development Kit10.
Quest’ultimo è disponibile solo sulla versione non FOSS del software, che è possibile installare tramite le repository open source linux.
In alternativa o anche parallelamente è possibile sviluppare codice Q# ed eseguirlo tramite Jupyter Notebook tramite Python.
Questo con i kernel necessari installati, avendo quindi l’ultima versione di dotnet disponibile.
Attualmente la versione LTS è la .NET Core 6.0 ed è quella che useremo.
Si può trovare direttamente sul sito della microsoft11 o più semplicemente tramite il package manager del proprio sistema operativo.
Altro passo necessario per l’esecuzione dei Jupyter Notebook è l’installazione delle runtime aspnet 12.
Una volta installata l’ultima versione di dotnet è possibile eseguire:
$ dotnet tool install -g Microsoft.Quantum.IQSharp
$ dotnet iqsharp install
Per alcune istallazioni linux sarà necessario eseguire in alternativa:
$ dotnet iqsharp install --user
Questo installa i kernel IQ# che useremo con i Jupyter Notebook.
Per l’installazione in locale di tutto ciò che è necessario per lo sviluppo di software in questo ambito e in altre applicazioni scientifiche risulta molto più semplice l’utilizzo di una distribuzione pre-impostata come quella di Anaconda13.
Uno strumento simile aiuta nella gestione di Python e altri strumenti software di ambito scientifico.
Se necessario lo si dovrà aggiungere al PATH 14:
$ PATH=/opt/anaconda/bin:$PATH
Tramite Anaconda si crea un ambiente di esecuzione con tutto quello che ci serve per i nostri obiettivi tramite il package manager incluso, conda:
$ conda create -n qsharp-env -c microsoft qsharp notebook
$ conda activate qsharp-env
In qualsiasi momento si può attivare l’ambiente conda che abbiamo creato per avere il necessario all’esecuzione dei nostri programmi Q# / Python.
Al momento della scrittura Anaconda supporta la versione di Python 3.9, per gli scopi di questa tesi si suppone di avere a disposizione almeno usa versione superiore alla 3 per garantire compatibilità.
L’esecuzione del software Q# può essere testato localmente predisponendo un ambiente di simulazione tramite il pacchetto Python chiamato qsharp.
import qsharp
from QsharpNamespace import Operation_One, Operation_Two
var1 = 10
print("Simulation started...")
Operation_One.simulate(par1=var1)
Operation_Two.simulate(par2=var1,par3=5)
Ad esempio come nel listato qui sopra utilizziamo uno script host.py per creare un ambiente di simulazione per poter eseguire le operazioni Q# definite in Operation_One e Operation_Two.
Il pacchetto automaticamente va a cercare nella directory locale le definizioni.
import qsharp
prepare_qubit = qsharp.compile("""
open Microsoft.Quantum.Diagnostics;
operation PrepareQubit(): Unit {
using (qubit = Qubit()) {
DumpMachine();
}
}
""")
if __name__ == "__main__":
prepare_qubit.simulate()
Un esempio più complesso può essere quello definito in qsharp-interop.py dove definiamo direttamente inline il contenuto del codice Q# che il package qsharp compila e simula.
Con il necessario installato è possibile leggere ed eseguire il codice di esempio pubblicato dagli autori di Learn Quantum Computing with Python and Q# sulla loro repository github15.
\(\pagebreak\)
Q#
Nei prossimi capitoli utilizzeremo Q# per implementare alcuni algoritmi quantistici. Per questo ci sarà utile introdurre delle basi in questo linguaggio per facilitare la lettura dei listati che saranno presentati successivamente.
Q# è il linguaggio di programmazione di algoritmi quantistici open source16 sviluppato da Microsoft, fa parte del Quantum Development Kit di quest’ultima.
Come linguaggio eredita caratteristiche classiche di linguaggi imperativi ad oggetti come Python, C# supportando loop, blocchi if/then e strutture dati di base.
Altre queste introduce in aggiunta costrutti specifici per le applicazioni nell’ambito della programmazione di algoritmi quantistici come ad esempio il repeat until success17 e la phase estimation18.
Il linguaggio è ad alto livello e agnostico riguardo l’hardware su cui verrà eseguito.

Figure 3: Diagramma che mostra i passaggi da idea a implementazione di un programma nel framework QDK, tratto dalla documentazione Microsoft QDK.
\pagebreak
Un semplice programma in Q# può essere:
namespace HelloQuantum {
open Microsoft.Quantum.Canon;
open Microsoft.Quantum.Intrinsic;
@EntryPoint()
operation SayHelloQ() : Unit {
Message("Hello quantum world!");
}
}
Questo stampa la stringa “Hello quantum world!”, EntryPoint indica al compilatore dove inizia l’esecuzione del programma.
Tra i tipi offerti dal linguaggio ci sono quelli classici: Int, Double, Bool, String.
Inoltre esistono dei tipi specifici al quantum computing: Result rappresenta il risultato di una misurazione di qubit e può avere solamente uno di due valori - One o Zero. Il linguaggio permette di specificare nuovi tipi per un proprio programma ma non offre feature di linguaggi come C# o Java come interfacce o classi.
I qubit vengono allocati tramite la keyword use. Se ne possono allocare uno o diversi alla volta.
use q = Qubit();
I principali attori di un programma che manipola qubit sono le cosiddette Operations, queste sono routine chiamabili di un programma che contengono operazioni quantistiche che manipolano lo stato del registro di qubit.
operation SayHelloQ() : Unit {
Message("Hello quantum world!");
}
\pagebreak Una parte fondamentale di un qualsiasi algoritmo quantistico è la misurazione dei qubit e la loro manipolazione. Per questo vengono utilizzate le misure di Pauli per misurazioni di singoli qubit secondo una data base.
operation MeasureOneQubit() : Result {
// Alloca un qubit, di default nello stato zero
use q = Qubit();
// Applichiamo Hadamard allo stato
// A seguito di questa operazione la misurazione
// potrebbe risultare 0 o 1 con uguale probabilità
H(q);
// Misuriamo in base Z il qubit
let result = M(qubit);
// Resettiamo il qubit prima di rilasciarlo
if result == One { X(qubit); }
return result;
}
Nel listato vediamo un esempio di misurazione in base Z di un qubit. Questa base di misurazione è spesso chiamata anche base computazionale.
Il qubit viene allocato, gli viene applicata la trasformata di Hadamard tramite la procedura H e poi viene misurato utilizzando M.
M effettua una misura di un singolo qubit in base Z di Pauli. Questa è del tutto equivalente a Measure([PauliZ], [qubit]).
L’operazione di misura è spesso seguita dal reset, quindi spesso è comodo l’utilizzo dell’operazione MResetX19, che si assicura che il qubit sia riportato allo stato \(|0\rangle\).
operation MResetX (target : Qubit) : Result
La misurazione di qubit ci fornisce dati in forma classica che potranno essere utilizzati nell’ambiente del chiamante dell’operazione normalmente secondo la logica classica.
\pagebreak
Oracoli
Per poter applicare l’algoritmo che andremo a descrivere e implementare in seguito è necessario creare dei cosiddetti oracoli delle funzioni che utilizzeremo come input. Prima definiamo cos’è un oracolo in questo contesto:
Un oracolo \(U_{f}\) è una matrice unitaria definita applicando \(f\) condizionatamente rispetto alle etichette assegnate agli stati dei
qubit. L’applicazione di un oracolo per due volte risulta nella matrice identità \(\mathbb{1}\).
Per ottenere questo è necessaria una manipolazione per convertire funzioni irreversibili in oracoli reversibili utilizzabili in ambito quantistico.
Questa manipolazione va fatta utilizzando le operazioni su qubit proprie di un simulatore o device quantistico come:
- \(\textsc{x}(t)\)
- questa operazione è l’equivalente del classico
NOT - \(\textsc{x}|0\rangle = |1\rangle\)
- \(\textsc{x}|1\rangle = |0\rangle\)
- questa operazione è l’equivalente del classico
- \(\textsc{cnot}(c,t)\)
- questa operazione è definibile come un
NOTcontrollato secondo l’input \(c\) - \(\textsc{cnot} |00\rangle = |00\rangle\)
- \(\textsc{cnot} |01\rangle = |01\rangle\)
- \(\textsc{cnot} |10\rangle = |11\rangle\)
- \(\textsc{cnot} |11\rangle = |10\rangle\)
- questa operazione è definibile come un
Dove \(t\) è il qubit target e \(c\) è il qubit di controllo per il Controlled-NOT.
- \(\textsc{swap}(t_{1},t_{2})\)
- come si può intuire dal nome scambia i valori dei
qubit - \(\textsc{swap} |10\rangle = |01\rangle\) e \(\textsc{swap} |01\rangle = |10\rangle\)
- come si può intuire dal nome scambia i valori dei
Le difficoltà maggiori nella definizione di oracoli per le funzioni che ci interessano le abbiamo con quelle costanti, questo in quanto passando da input a output si perde l’informazione dell’input utilizzato. Rendendo tali funzioni irreversibili.
Fortunatamente esiste una tecnica generale per rendere una funzione classica irreversibile \(f: Bool \to Bool\) in una funzione classica reversibile \(g\). \[h(x,y) = (x,y \oplus f(x))\] Questa nuova funzione \(h\) aggiunge al input originario di \(f\) \(x\) un nuovo input \(y\) che non è altro che il valore di output che andrà a modificare tramite l’operazione \(\oplus\)20.
Questa stessa tecnica è utilizzabile per definire un oracolo \(U_{f}\): \[U_{f} |x \rangle | y \rangle = | x \rangle | y \oplus f(x) \rangle\]
In questo modo manteniamo traccia dell’input \(x\) che altrimenti andrebbe perso dopo l’applicazione di \(f\).
Gli oracoli che utilizziamo per testare gli algoritmi definiti nelle prossime sezioni sono riportati nel listato oracles.qs (Listing 3).
operation ApplyZeroOracle(
control : Qubit, target : Qubit) : Unit {
}
operation ApplyOneOracle(
control : Qubit, target : Qubit) : Unit {
X(target);
}
operation ApplyZeroOracleN(
control : Qubit[], target : Qubit) : Unit {
}
operation ApplyOneOracleN(
control : Qubit[], target : Qubit) : Unit {
X(target);
}
operation ApplyIdOracle(
control : Qubit, target : Qubit) : Unit {
CNOT(control,target);
}
operation ApplyXOROracleN(
control : Qubit[], target : Qubit) : Unit {
for qubit in control {
CNOT(qubit,target);
}
}
operation ApplyNotOracle(
control : Qubit, target : Qubit) : Unit {
X(control);
CNOT(control,target);
X(control);
}
Qui sopra sono definite le versioni a singolo qubit e a n-qubit degli oracoli quantistici di alcune funzioni booleane costanti e bilanciate, definiamo cosa siano funzioni di questo tipo nel prossimo capitolo. Tutte queste funzioni hanno tipo \[f: Bool^n \to Bool\]
In particolare abbiamo definito oracoli per le seguenti funzioni:
- \(f_{1}(x)=0\)
- \(f_{2}(x)=1\)
- \(f_{3}(x)=x\)
- \(f_{4}(x)= \lnot x\) ovvero \(f_{4}(x) = 1-x\)
- \(f_{5}(x) = \oplus_{i=0}^{n-1} x_{i}\)
- dove \(x\) è l’input lungo \(n\)
qubit
- dove \(x\) è l’input lungo \(n\)
In questi casi le prime due funzioni sono costanti e le restanti sono bilanciate.
È facile verificare che gli oracoli definiti in Q# corrispondono alle funzioni sopra definite, in particolare:
ApplyZeroOraclee la sua versione a \(n\)qubitequivalgono a \(f_{1}\)ApplyOneOraclee la sua versione a \(n\)qubitequivalgono a \(f_{2}\)ApplyIdOracleequivale all’identità \(f_{3}\)ApplyNotOracleequivale a \(f_{4}_{}\)ApplyXOROracleNequivale a \(f_{5}\)
In figura 1 vediamo un altro esempio di oracolo bilanciato che applica 3 porte CNOT all’ultimo qubit:
- \(q_{3} = q_{3} \oplus q_{0}_{} \oplus q_{1} \oplus q_{2}\)
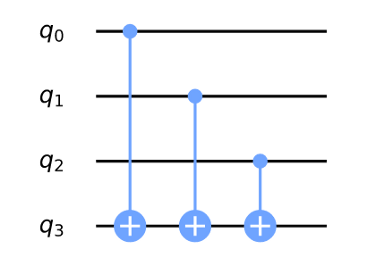
Figure 4: esempio di oracolo bilanciato utilizzando porte CNOT
La precedente definizione single qubit di \(U_{f}\) può essere estesa per il caso di \(f\) con \(n\) qubit
\[f(x_{0}, x_{1},\cdots,x_{n-1})\]
in questa maniera:
\[U_{f}|x_{0} x_{1}\cdots x_{n-1}y\rangle = | x_{0} x_{1}\cdots x_{n-1}\rangle \otimes | f(x_{0}, x_{1},\cdots,x_{n-1}) \oplus y\rangle\]
\(\pagebreak\)
Il nome oracolo deriva da una convenzione di nomenclatura nell’ambito della Teoria della Complessità. In particolare è stata definita in quanto una classe di complessità \(A\) può essere convertita in una nuova classe di problemi \(A^{\textsc{b}}\), che permettono ad \(A\) di risolvere problemi di tipo \(B\) in un singolo passo, proprio come se stesse consultando un oracolo.
Una macchina oracolo si può immaginare come una macchina di Turing connessa a un oracolo, in questo contesto si intende con oracolo una entità blackbox in grado di risolvere un qualche problema. Questo problema non deve per forza essere computabile in quanto l’oracolo non è una reale macchina o programma ma semplicemente una scatola oscura che produce una soluzione corretta per ogni istanza del problema computazionale in un singolo passo.21 \(\pagebreak\)
Algoritmo di Deutsch-Jozsa
L’algoritmo di Deutsch-Jozsa ha interesse storico in quanto primo algoritmo quantistico in grado di superare in performance il miglior algoritmo classico corrispondente, mostrando che possono esistere vantaggi nel calcolo quantistico. Questo algoritmo ha spinto la ricerca in questa direzione per determinati problemi.
L’algoritmo risponde a una domanda su una funzione \(f\) booleana con \(n\) bit in input \[f: Bool^n \to Bool\] \[f(\{x_{0},x_{1},\cdots,x_{n}\}) \rightarrow 0\text{ o }1\]
Questa funzione su cui agisce l’algoritmo ha la proprietà di essere una di due forme:
- costante
- bilanciata
Definite come:
- Una funzione è costante se restituisce per tutti gli input \(\{x_{0},x_{1},\cdots,x_{n}\}_{}\) lo stesso risultato
- Una funzione è bilanciata se restituisce 0 esattamente per metà degli input, e 1 esattamente per metà degli input
Il problema di Deutsch-Jozsa è stato ideato per essere facile da risolvere con una soluzione algoritmica quantistica ed essere difficile per qualsiasi algoritmo classico.
Questo per dimostrare che un problema cosiddetto blackbox può essere risolto efficientemente e senza errore da un computer quantistico, risultato non possibile tramite un computer classico.
In particolare questo risultato mostra che la classe computazionale \(EQP\) (a volte chiamata \(QP\)) Exact Quantum Polynomial Time è distinta da \(P\) ovvero la classe dei problemi risolvibili classicamente in tempo polinomiale.
\(\pagebreak\)
La Soluzione Classica
Nella soluzione classica nel caso migliore due query all’oracolo sono sufficienti per riconoscere la funzione \(f\) come bilanciata. Per esempio supponiamo di avere due chiamate con i seguenti risultati: \[f(0,0,\cdots) \rightarrow 0\] \[f(1,0,\cdots) \rightarrow 1\]
Dato che è assunto che \(f\) sia garantita essere costante oppure bilanciata questi risultati ci dimostrano \(f\) come bilanciata.
Per quanto riguarda il caso peggiore tutte le nostre interrogazioni daranno lo stesso output, decidere in modo certo che \(f\) sia costante necessita di metà più uno interrogazioni. Dato che il numero di input possibili è \(2^{n}\) questo significa che, nel caso peggiore, saranno necessarie \(2^{n-1}+1\) interrogazioni per essere certi che \(f(x)\) sia costante.
È possibile una soluzione probabilistica tramite un algoritmo randomizzato, con un numero costante di valutazioni \(k\) è possibile produrre un risultato con alta probabilità corretto.
Dato \(k\ge 1\), un algoritmo di questo tipo fallisce con probabilità \[\epsilon \le \frac{1}{2^{k}}\] In ogni caso l’unico modo per avere un risultato certo rimane avere \(k = 2^{n-1} + 1\).
La complessità di questi algoritmi rimane \(\textsc{time} = O(2^{n}})\) e quindi difficili da trattare al crescere della lunghezza dell’input.
\(\pagebreak\)
La Soluzione Quantistica
La soluzione di David Deutsch e Richard Jozsa del 1992, poi migliorata nel 1998 è molto più efficace delle alternative classiche.
Tramite la computazione quantistica è possibile risolvere questo problema con un’unica chiamata della funzione \(f(x)\). Questo a patto che la funzione \(f\) sia implementata come un oracolo quantistico \(U_{f}\), che mappi: \(|x\rangle | y \rangle\) a \(| x \rangle |y \oplus f(x) \rangle\) 20
I passi dell’algoritmo in particolare sono:
- prepara 2 registri di
qubit, il primo di \(n\)qubitinizializzato a \(| 0 \rangle\) e il secondo di un singoloqubitinizializzato a \(| 1\rangle\) - applica
Hadamarda entrambi i registri - applica l’oracolo quantistico \(U_{f}\) definito per \(f\)
- a questo punto il secondo registro può essere ignorato, riapplica
Hadamardal primo registro - misura il primo registro, questo risulta nello stato 0 per \(f(x)\) costante e diversamente nel caso bilanciato
Nei listati successivi riportiamo l’implementazione Q# della versione a singolo qubit e la generalizzazione nel caso di \(n\)-qubit.

Figure 5: i passi dell’algoritmo n-qubit in forma di circuito
\pagebreak
Un punto fondamentale dell’algoritmo è l’utilizzo della porta Hadamard, chiamata anche trasformata di Hadamard.
Questa è una generalizzazione delle trasformate di Fourier definita dalla matrice \(H_{m} = 2^{m} \times 2^{m}\).
Questa è definibile ricorsivamente a partire dall’identità \(H_{0} = 1\), per \(m > 0\):
\begin{align*}
H_{m} = \frac{1}{\sqrt{2}}
\begin{pmatrix}
H_{m-1} & H_{m-1} \\
H_{m-1} & -H_{m-1}
\end{pmatrix}
\end{align*}
e quindi alcuni esempi di porte di Hadamard sono:
\begin{align*}
H_{0} &= +(1) \\
H_{1} &= \frac{1}{\sqrt{2}}
\begin{pmatrix}
1 & 1 \\
1 & -1
\end{pmatrix} \\
H_2 &= \frac{1}{2}
\begin{pmatrix}
1 & 1 & 1 & 1\\
1 &-1 & 1 & -1\\
1 & 1 & -1 & -1\\
1 & -1 & -1 & 1\\
\end{pmatrix} \\
\end{align*}
Il trasformato di Hadamard \(H_{1}\) è la porta logica quantistica conosciuta come porta Hadamard, l’applicazione di questa porta a ciascun qubit di un registro a n-qubit parallelamente è equivalente alla trasformata \(H_{n}\).
Applicando un circuito di Hadamard a un qubit nello stato \(| 0 \rangle\) si crea uno stato sovrapposto tra gli stati \(| 0 \rangle\) e \(| 1 \rangle\) denominato \(| + \rangle\).
A livello matematico sono definite:
\[ | + \rangle = \frac{1}{\sqrt{2}} (| 0 \rangle + | 1 \rangle)\]
\[ | - \rangle = \frac{1}{\sqrt{2}} (| 0 \rangle - | 1 \rangle)\]

Figure 6: Rappresentazione geometrica di un qubit con la sfera di Bloch. Sono rappresentati come poli sull’asse (z) gli stati equivalenti allo 0 e 1 di un bit classico, sull’asse (x) invece i poli sono gli stati sopraccitati (| + rangle) e (| - rangle). Con questa rappresentazione è possibile notare come (H) non sia altro che una rotazione in questo spazio tridimensionale.
Inoltre con una funzione \(f\) applicata a questa sovrapposizione si ottiene, nel caso \(n=1\), uno stato sovrapposto tra \(f(0)\) e \(f(1)\).
Questo effetto è utilizzato dall’algoritmo in quanto riapplicando Hadamard si controlla in un solo passo se si ottiene la sovrapposizione di due stati uguali o di due stati diversi, o meglio se \(f(0) = f(1)\) o meno. La riapplicazione di \(H\) restituirà \(1\) nel primo caso, \(0\) nel secondo.
\(\pagebreak\)
Seguono i calcoli per il caso a \(1\) qubit: L’obiettivo è controllare la condizione \(f(0) = f(1)\), equivalente a controllare \(f(0) \oplus f(1)\).
In questo caso lo XOR è implementato come una Controlled NOT gate CNOT.
Lo stato iniziale aggiungendo un qubit di controllo è \(|0 \rangle |1\rangle\), si applica Hadamard a entrambi:
\[\frac{1}{2} (| 0 \rangle + | 1 \rangle) (| 0 \rangle - |1 \rangle\]
Data l’implementazione quantistica in forma di oracolo \(U_{f}\) della funzione iniziale \(f\), che ricordiamo è definita come una mappa tra \(|x\rangle | y \rangle\) e \(|x \rangle | f(x) \oplus y \rangle\) La applichiamo allo stato ottenuto:
\begin{align*}
\frac{1}{2} ( |0\rangle (| f(0)& \oplus 0 \rangle - | f(0) \oplus 1 \rangle ) + |1\rangle (| f(1) \oplus 0 \rangle - | f(1) \oplus 1 \rangle) ) \\
=& \frac{1}{2} ((-1)^{f(0)} | 0 \rangle ( |0 \rangle - |1\rangle) + (-1)^{f(1)} | 1 \rangle (|0 \rangle - |1 \rangle)) \\
=& (-1)^{f(0)} \frac{1}{2} ( | 0 \rangle + (-1)^{f(0) \oplus f(1)} |1\rangle) (|0\rangle - |1\rangle)
\end{align*}
La fase globale \(-1\) e il secondo qubit finale vengono ignorati, a questo punto della computazione si ha lo stato:
\[ \frac{1}{\sqrt{2}} (|0\rangle + (-1)^{f(0) \oplus f(1)} |1 \rangle)\]
Applicando nuovamente Hadamard otteniamo:
\begin{align*}
\frac{1}{2} (|0\rangle + |1 \rangle &+ (-1)^{f(0)\oplus f(1)} |0\rangle - (-1)^{f(0)\oplus f(1)} |1\rangle)\\
=& \frac{1}{2} ((1 + (-1)^{f(0)\oplus f(1)} ) | 0\rangle + (1 - (-1)^{f(0)\oplus f(1)} | 1 \rangle)
\end{align*}
A questo punto viene misurato il qubit:
- \(f(0) \oplus f(1) = 0\) se e solo se misuriamo \(|0\rangle\)
- \(f(0) \oplus f(1) = 1\) se e solo se misuriamo \(|1\rangle\)
Concludiamo che sappiamo con certezza se \(f(x)\) è costante o bilanciata in un singolo uso della blackbox \(U_g\).
Nel listato seguente vediamo l’implementazione in Q# dell’algoritmo in questo caso. Al qubit viene applicato H e poi viene utilizzata la funzione oracolo, di queste vi rimandiamo alle definizioni nel capitolo 4. L’algoritmo ritorna True nel caso la funzione sia bilanciata, False altrimenti.
operation DeutschJozsaSingleBit(
oracle : (( Qubit, Qubit ) => Unit)) : Bool {
use control = Qubit();
use target = Qubit();
H(control);
X(target);
H(target);
oracle(control, target);
H(target);
X(target);
return MResetX(control) == One;
}
\(\pagebreak\)
Il caso \(n=2\) qubit non è diverso:
L’algoritmo inizia nello stato di \(n + 1\) qubit \(|00\rangle|1\rangle\).
Applicando Hadamard si ottiene lo stato
\[\frac{1}{\sqrt{2^{3}}} \sum_{x=0}^{2^{2}-1} |x\rangle(|0\rangle - | 1 \rangle) \]
Dove la sommatoria esprime le configurazioni \(x\) in qubit da \(0\) a \(3\)
\[|00\rangle, |01\rangle,|10\rangle, |11\rangle\]
Per ciascuna di queste \(x\), \(f(x)\) vale \(0\) oppure \(1\), dato ciò la formula precedente equivale a \[\frac{1}{\sqrt{2^{3}}} \sum_{x=0}^{3}^{} (-1)^{f(x)} |x\rangle (|0\rangle - |1\rangle)\]
A questo punto l’ultimo qubit \( \frac{|0\rangle - | 1 \rangle}{\sqrt{2}}\) possiamo ignorarlo, ottenendo
\[\frac{1}{\sqrt{2^{^{2}}}} \sum_{x=0}^{3} (-1)^{f(x)} |x\rangle\]
Riapplichiamo Hadamard a tutti gli \(n=2\) qubit
\begin{align*}
&\frac{1}{\sqrt{2^{^{2}}}} \sum_{x=0}^{3} (-1)^{f(x)} \left[\frac{1}{\sqrt{2^{^{2}}}} \sum_{y=0}^{3} (-1)^{x\cdot y} |y\rangle\right] \\
=&\frac{1}{2^{^{2}}} \sum_{y=0}^{3} \left[ \sum_{x=0}^{3} (-1)^{f(x)}(-1)^{x\cdot y}\right] |y\rangle
\end{align*}
Dove \(x \cdot y = x_{0}y_{0} \oplus x_{1}y_{1} \oplus x_{2}y_{2} \oplus x_{3}y_{3}\), somma modulo \(2\) del prodotto bit a bit.
Data questo risultato la probabilità di misurare \(|00\rangle\) è \[\left| \frac{1}{2^{^{2}}} \sum_{x=0}^{3} (-1)^{f(x)} \right|^{2}\] Che risulta \(1\) se \(f(x)\) è costante e \(0\) se altrimenti \(f(x)\) è bilanciata.
In altre parole, la misura finale sarà \(|00\rangle\) se \(f(x)\) è costante e un qualche altro stato nel caso in cui \(f(x)\) sia bilanciata. Nel listato successivo riportiamo l’algoritmo per questo caso. Valgono le stesse considerazioni che per il caso a un singolo qubit. \pagebreak
operation DeutschJozsa(
size : Int, oracle : ((Qubit[], Qubit ) => Unit) ) : Bool {
use control = Qubit[size];
use target = Qubit();
ApplyToEachA(H, control);
X(target);
H(target);
oracle(control, target);
H(target);
X(target);
let result = MResetX(control[0]) == One;
ResetAll(control);
return result;
}
\(\pagebreak\)
\(\pagebreak\)
Teletrasporto Quantistico
Concludiamo la nostra trattazione mostrando un interessante fenomeno quantistico che riguarda la sovrapposizione di più stati, la correlazione quantistica o entanglement quantistico.
Il termine entanglement, traducibile come groviglio in italiano, fu introdotto dal nobel per la fisica Erwin Schrödinger, i cui contributi alla meccanica quantistica furono fondamentali e indica la forte relazione che due particelle entangled in un sistema quantistico mantengono secondo la legge di conservazione.
Questa legge continua a valere senza alcun limite spaziale, permettendo che la misura di una singola particella influenzi istantaneamente il corrispondente valore dell’altra. \par Un altro risultato fondamentale della meccanica quantistica sono il teorema di no-cloning e quello di non discriminazione. Il primo vieta la creazione di un duplicato esatto di uno stato quantistico sconosciuto, il secondo afferma che dati due stati quantistici non ortogonali di un sistema non sia possibile distinguerli con certezza.
Non siamo in grado di distinguere due particelle elementari: se queste fossero scambiate sarebbe impossibile accorgersene. Non ha senso affermare che le particelle elementari abbiano una individualità.
È più corretto affermare che le due posizioni nello spazio hanno la proprietà di avere campi quantistici nello stesso stato.
Partendo da uno stato entangled è però possibile teletrasportare lo stato di una particella \(A\) in una particella \(B\).
Per effetto del teletrasporto lo stato di \(B\) sarà esattamente quello che aveva \(A\) precedentemente all’operazione.
In letteratura questi attori sono spesso soprannominati Alice e Bob.
Lo stesso risultato si potrebbe avere trasportando fisicamente \(A\) al posto di \(B\). Per le proprietà dell'entanglement non c’è un limite spaziale al teletrasporto quantico.
Gli schemi per effettuare questa operazione sono diversi, noi riportiamo quello più semplice: il teletrasporto di un qubit.
\(\pagebreak\)

Figure 7: Trasposizione in circuito delle operazioni necessarie al teletrasporto quantistico.
Definiamo:
- \(| \psi \rangle_{A1} = \alpha |0 \rangle_{A1} + \beta|1\rangle_{A1}\) è il generico stato da teletrasportare
- \(A2\)
qubitentangled diAlice - \(B\)
qubitentangled diBob
Lo stato si inizializza in \[ \frac{1}{\sqrt{2}} | \psi \rangle_{A1} (|0\rangle_{A2} | 1 \rangle_{B} - |1\rangle_{A2} |0\rangle_{B})\]
Si riscrive lo stato complessivo in
\begin{align*}
- \frac{1}{2}( |0\rangle_{A1} |1\rangle_{A2} - |1\rangle_{A1} |0\rangle_{A2})(\alpha |0\rangle_{B} + \beta |1\rangle_{B}) \\
- \frac{1}{2}( |0\rangle_{A1} |1\rangle_{A2} - |1\rangle_{A1} |0\rangle_{A2})(\alpha |0\rangle_{B} - \beta |1\rangle_{B}) \\
- \frac{1}{2}( |0\rangle_{A1} |0\rangle_{A2} - |1\rangle_{A1} |1\rangle_{A2})(\beta |0\rangle_{B} + \alpha |1\rangle_{B}) \\
- \frac{1}{2}( |0\rangle_{A1} |0\rangle_{A2} - |1\rangle_{A1} |1\rangle_{A2})(\beta |0\rangle_{B} - \alpha |1\rangle_{B}) \end{align*}
Alice può ridurre attraverso una misura di Bell lo stato di Bob a uno dei quattro stati con coefficienti \(\alpha\) e \(\beta\). Bob non può comunque ancora distinguere in quale dei quattro stati il proprio qubit si trovi, per questo è necessario un ulteriore passo.
La trasmissione dell’informazione avviene quando Alice comunica a Bob il risultato della misura.
A questo punto Bob può effettuare una trasformazione unitaria opportuna che trasformi il proprio stato in quello stato \(|\psi\rangle\) originario.
Questo ultimo passaggio è fondamentale: per poter ricostruire lo stato iniziale il destinatario deve conoscere il risultato di una misurazione del mittente, questa informazione viene trasmessa attraverso un mezzo di trasmissione classico. La trasmissione di questa misura limita la velocità del teletrasporto che non è quindi istantaneo, ma limitato dalla velocità della luce in accordo con la relatività speciale.
La misurazione da parte di Alice porta alla perdita dello stato iniziale rispettando quindi il teorema di no-cloning citato precedentemente.
Molti esperimenti sono stati effettuati nell’ambito del teletrasporto quantistico, l’attuale record di distanza per un esperimento di questo tipo è stato registrato in un esperimento all’aperto che ha avuto luogo nelle isole Canarie e teletrasportò particelle tra due osservatori astronomici dell'Instituto de Astrofísica de Canarias ad una distanza di 143Km.22

Figure 8: Il teletrasporto quantistico agisce in accordo alla relatività speciale con l’utilizzo di due canali di comunicazione, uno classico e una quantistico.
Nei listati 6 e 7 sono riportate le implementazioni dell’algoritmo di teletrasporto quantistico rispettivamente in Python e Q#. I parametri utilizzati nel caso del primo sono:
msg, il qubit che vogliamo muoverehere, il qubit temporaneothere, il qubit di destinazione
Per il secondo sono:
msg, il qubit che vogliamo muoveretarget, il qubit di destinazione
Nel algoritmo in Q# il qubit temporaneo è istanziato nella variabile register.
L’unica differenza nei due programmi è l’uso della funzione di libreria Q# MResetZ per la misura e il reset dei qubit in un’unica chiamata.
from interface import QuantumDevice, Qubit
from simulator import Simulator
# parametri:
# msg qubit che vogliamo muovere
# here qubit temporaneo
# there qubit di destinazione
# here, there sono inizializzati nello stato |0〉
def teleport(msg: Qubit, here: Qubit, there: Qubit) -> None:
here.h()
here.cnot(there)
msg.cnot(here)
msg.h()
# Il risultato della misura è informazione classica
# che verrà trasmessa al ricevente attraverso un
# mezzo di comunicazione classico
if msg.measure(): there.z()
if here.measure(): there.x()
msg.reset()
here.reset()
namespace Microsoft.Quantum.Samples.Teleportation {
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Canon;
open Microsoft.Quantum.Measurement;
operation Teleport (msg : Qubit, target : Qubit) :
Unit {
use register = Qubit();
H(register);
CNOT(register, target);
CNOT(msg, register);
H(msg);
// misurando con MResetZ resettiamo nello
// stesso passo i qubit misurati rendendoli
// utilizzabili nuovamente se necessario
if (IsResultOne(MResetZ(msg))) { Z(target); }
if (IsResultOne(MResetZ(register))) { X(target); }
}
}
\(\pagebreak\)
Conclusioni
L’area di ricerca sui fenomeni quantistici e le sue possibilità a livello computazionale è in crescita e offre grandi possibilità e spunti in quanto relativamente giovane, nascendo negli anni 80 con il primo modello quantistico della macchina di Turing23 creato dal fisico Paul Benioff.
L’Unione Europea ha inserito lo sviluppo delle tecnologia di quantum computing tra gli obiettivi strategici del Decennio Digitale Europeo, in cui la Commissione Europea presenta una strategia per lo sviluppo e la digitalizzazione da raggiungere dagli stati membri nel entro il 2030.
Inoltre sempre su questo tema gli stati membri hanno firmato la Dichiarazione Europea sull’Infrastruttura per la Comunicazione Quantistica - EuroQCI - per costruire una rete di comunicazione condivisa tra le macchine quantistiche sul territorio.
Tutto questo per garantire competitività tecnologica sul piano mondiale, anche a livello di cybersicurezza nel cui ambito sono tanti gli sforzi di ricerca in campo quantistico.
Importante il recente risultato dei fisici A. Aspect, J. Clauser e A. Zeilinger che con i loro esperimenti sulla sovrapposizione dei fotoni sviluppando la teoria di John Bell sull’esistenza di variabili nascoste con la proposta della disugualianza di Bell.24 I tre hanno dimostrato sperimentalmente la bontà delle regole della fisica quantistica, violando la disugualianza di Bell. Questo indica come la meccanica quantistica non possa essere sostituita da una teoria che utilizza variabili nascoste, riscontro che è valso loro il nobel per la fisica.25
Dopo 50 anni in cui la velocità di calcolo dei calcolatori classici ha continuato a crescere raddoppiando circa ogni due anni - in accordo con la legge di Moore - i componenti dei computer stanno raggiungendo i limiti fisici del progresso tecnologico e ingegneristico in quella direzione, con componentistiche nelle dimensioni dell’atomo. Dalla ricerca nel campo il consenso volge verso il cominciare a pensare a un post-Moore. I limiti fisici, da quelli termici a quelli energetici, è probabile siano raggiunti nei prossimi 30-40 anni, le roadmap dell’industria per i prossimi decenni non si basano più sulla famosa legge ma piuttosto sull’innovazione nei device - sempre più mobili - e nei loro sensori.26 , 27
Per questo negli ultimi anni è cresciuta la necessità di sviluppare nuovi modelli computazionali che permettano di andare oltre il modello classico.
È da questa necessità che negli ultimi anni l’interesse per le tecnologie quantistiche è cresciuto rapidamente e certamente continuerà a evolversi intanto che il computer classico potrebbe essere vicino a raggiungere i propri limiti fisici.
\(\pagebreak\)
Bibliografia
- Sarah C. Kaiser, Christopher Granade - Learn Quantum Computing with Python and Q#, Manning 2021 (https://www.manning.com/books/learn-quantum-computing-with-python-and-q-sharp)
- J. S. Bell - On the Einstein Podolsky Rosen Paradox, 1964 (https://www.informationphilosopher.com/solutions/scientists/bell/Bell_On_EPR.pdf)
- S. Kumar - Fundamental Limits to Moore’s Law, 2015 (https://arxiv.org/abs/1511.05956)
- Nature 530 (7589) - The chips are down for Moore’s Law (https://www.nature.com/news/the-chips-are-down-for-moore-s-law-1.19338)
- Paul Benioff - The computer as a physical system (https://link.springer.com/article/10.1007/BF01011339)
- https://github.com/crazy4pi314/learn-qc-with-python-and-qsharp
- https://ieeexplore.ieee.org/document/9274431
- https://learn.microsoft.com/en-us/azure/quantum/install-overview-qdk
- https://github.com/microsoft/quantum/tree/main/samples/getting-started/teleportation
- https://azure.microsoft.com/en-us/resources/development-kit/quantum-computing/
- https://qiskit.org/textbook/ch-algorithms/deutsch-jozsa.html
- https://www.nobelprize.org/prizes/physics/2022/press-release/
- https://en.wikipedia.org/wiki/Oracle_machine
-
https://www.manning.com/books/learn-quantum-computing-with-python-and-q-sharp ↩︎
-
documentazione azure: https://learn.microsoft.com/en-us/azure/quantum/install-overview-qdk ↩︎
-
https://azure.microsoft.com/en-us/resources/development-kit/quantum-computing/ ↩︎
-
Si trovano informazioni a riguardo di questa distribuzione software all’indirizzo https:www.anaconda.com ↩︎
-
Supponiamo l’uso di un ambiente
unix↩︎ -
https://github.com/crazy4pi314/learn-qc-with-python-and-qsharp ↩︎
-
https://learn.microsoft.com/en-us/azure/quantum/user-guide/language/statements/conditionalloops ↩︎
-
Per approfondire a riguardo si può leggere la documentazione di Microsoft Azure: https://learn.microsoft.com/en-us/azure/quantum/user-guide/libraries/standard/algorithms#quantum-phase-estimation. L’algoritmo di stima della fase quantistica o stima dell’autovalore quantistico è utilizzato per stimare con alta probabilità dato un errore le operazioni di operatori unitari \(U\) e \(m\) qubit. La phase estimation è spesso una subroutine di altri algoritmi quantistici, per esempio l’algoritmo di Shor, ed è un’altra applicazione della trasformata di Fourier che nominiamo nel capitolo 5 parlando della trasformata di Hadamard. ↩︎
-
https://learn.microsoft.com/en-us/qsharp/api/qsharp/microsoft.quantum.measurement.mresetx ↩︎
-
dove \(\oplus\) è l’addizione modulo \(2\) o
XOR↩︎ -
Nature 489 (7415) - Quantum teleportation over 143 kilometres using active feed-forward ↩︎
-
Paul Benioff - The computer as a physical system (https://link.springer.com/article/10.1007/BF01011339) ↩︎
-
J. S. Bell - On the Einstein Podolsky Rosen Paradox, 1964 (https://www.informationphilosopher.com/solutions/scientists/bell/Bell_On_EPR.pdf) ↩︎
-
https://www.nobelprize.org/prizes/physics/2022/press-release/ ↩︎
-
S. Kumar - Fundamental Limits to Moore’s Law, 2015 (https://arxiv.org/abs/1511.05956) ↩︎
-
Nature 530 (7589) - The chips are down for Moore’s Law (https://www.nature.com/news/the-chips-are-down-for-moore-s-law-1.19338) ↩︎