Reti Neurali & Deep Learning
- Prof.essa Valentina Gliozzi, Prof.essa Rossella Cancelliere
- https://transno.com/doc/3y-nWb7O0Jl
Principi
- le reti neurali sono strutture che simulano il comportamento del cervello umano
- in particolare l’unita' base: il neurone
- funzioni: raccoglie, elabora, propaga segnali
- in particolare l’unita' base: il neurone
La struttura in particolare e' composta da diverse parti:
- neuroni di input
- neurone di output
- a questo e' associato un ulteriore input: il bias
- la tendenza ad attivarsi
- a questo e' associato un ulteriore input: il bias
- la somma pesata viene passata a una funzione di attivazione, da questa deriva il risultato
Una rete neurale (NN) e' un modello computazionale composto da neuroni artificiali, le sue proprieta' sono:
- non linearita', la funzione che elabora la risposta non e' lineare
- input-output mapping, ha un ingresso e un’uscita
- fault tolerance, il task sulla quale e' addestrata e' distribuito
- incremental training, possibile continuare l’addestramento nel momento in cui ci siano nuovi dati
Un NN puo' essere
- supervisionato
- insieme di addestramento con input e output desiderato
- usi in classificazione, riconoscimento, diagnostica, regressione
- non supervisionato
- insieme di addestramento non etichettati
- usi in clustering
Architetture
- single layer feed forward
- grossi limiti, sorpassato
- multi layer feed forward
- livelli nascosti, non interagiscono direttamente con il mondo esterno
- recurrent
- livelli nascosti
- feedback loop
Perceptron
Primo esempio di rete neurale (1958), può risolvere semplici problemi di classificazione nel caso in cui il problema sia linearmente separabile.
Un problema si dice linearmente separabile se i dati rappresentati nello spazio sono divisibili nelle loro classi tramite una linea retta, detta decision boundary.
La rete del perceptron e' semplice, con \(p-1\) neuroni di input e un neurone di bias. Il neurone di output effettua la somma pesata, detta campo locale: \[v_{}_{j} = \sum^{p}_{i=0} w_{ji}x_{i}\]
La funzione di attivazione:
\begin{math}
\phi(v_{j}) =
\begin{cases}
1 \qquad \text{se } v_{j} > 0 \\
-1 \qquad \text{altrimenti}
\end{cases}
\end{math}
L’apprendimento e' effettuato tramite un’algoritmo iterativo dove \(\eta\) e' il learning rate:
\begin{algorithm} \caption{Algoritmo di Apprendimento del Percettrone} \begin{algorithmic}[1] \Procedure{Learning-Perceptron} \State{n \gets 0} \State{\text{inizializza } w(n) \text{ casualmente}} \While{\text{ci sono esempi classificati erroneamente}} \State{(x(n),d(n))\gets \text{esempio mis-classificato}} \If{d(n) = 1} \State{w(n+1)\gets w(n) + \eta x(n)} \EndIf \If{d(n)=-1} \State{w(n+1)\gets w(n) - \eta x(n)} \EndIf \State{n \gets n +1} \EndWhile \end{algorithmic} \end{algorithm}
Con il cambiamento dei pesi \(w\) si sta spostando la decision boundary, tracciata perpendicolarmente al vettore dei pesi.
L’algoritmo si ferma quando tutti gli elementi del training set sono classificati correttamente. A quel punto la configurazione di pesi e' corretta.
Teorema di Convergenza
Se esiste una soluzione - quindi le due classi sono linearmente separabili - l’algoritmo di apprendimento termina, trovandola.
Geometricamente, se \(w \cdot x > 0 \land -90 < \alpha < \180\) \[w(n) \cdot x(n) = ||w|| \cdot ||x|| \cos (\alpha)\]
Quindi la modifica del vettore pesi porta a cambiare la decision boundary (retta perpendicolare al vettore pesi) che accomodi l’input mal classificato corrente. Lo spostamento della boundary puo' causare altri input ad essere mal classificati.
Inizialmente i pesi sono posti a 0. La dimostrazione procede portando tutti i dati in un’unica classe \(C\) che unisca \(C_{1}\) e \(C_{}_{}_{}_{}_{}_{2}\) (in questo caso si restituisce 1 a \(\lnot x\)) e mostrando che esistono un lower bound \(\alpha\) e un upper bound \(\beta\) al numero di passi di iterazione \(k\).
Per la sequenza di stimoli vengono modificati i pesi
\begin{align*}
w(1) = w(0) + x(0) \\
w(2) = w(1) + x(1) \\
\cdots \\
w(k+1) = w(k) + x(k)
\end{align*}
In quanto \(k\) ha un lower bound quadratico all’infinito e un upper bound \(k\) non puo' crescere all’infinito, pena l’inconsistenza di questi limiti.
- \[\alpha = \min{(w^{*T} x(i))} \qquad (\forall i \in 0\dots k)\]
- \[\beta = (\max{||x(i)||})^2 \qquad (\forall x(i) \in C)\]
\[k \le \frac{ \beta|| w^{*} ||^2 }{\alpha^{}^2}\]
XOR
Un classico problema non linearmente risolvibile e' quello dello XOR. Questo problema rimase aperto per un periodo, portando ad una crisi nella ricerca che apri' la strada a nuove strutture per i NN.
Multilayer Perceptron
Nel 1969 l’entusiasmo iniziale viene meno quando si mostrano molti problemi non linearmente separabili a cui i percettroni non potevano dare soluzione. Le reti multilivello permettono di discriminare aree convesse nello spazio, superando i limiti dei percettroni singoli.
Adaline
Adaptive Linear Neural
Questa struttura modifica come vengono aggiornati i pesi, si focalizza sulla riduzione dell’errore.
- mentre il percettrone aveva l’obiettivo di diminuire gli input misclassificati
- qui l’obiettivo e' la riduzione dell’errore globale
L’architettura del neurone e' differente, non più una funzione di attivazione ma una funzione lineare.
Si studia la derivata di errore in relazione al peso, se la derivata e' negativa allora la funzione errore sta diminuendo, si continua ad aumentare il peso. Se la derivata e' positiva l’errore e' in salita e si diminuisce il peso.
Formalmente si descrivono le coppie features-valore nell’esempio \(k\): \[(x^{k} , d^{k})\] L’errore viene definito come
\begin{align*}
E^{k} (w) &= \frac{1}{2}(d^{k} - y^{k})^{2} \\
&= \frac{1}{2}(d^{k} - \sum^{m}_{j=0} x^{k}_{j} w_{j})^{2}
\end{align*}
Quindi definiamo l’errore per l’esempio \(k\) come la differenza tra il valore desiderato \(d^{k}\) e quello ottenuto \(y^{k}\). Quindi l’errore totale sulla rete e' \[E_{\text{tot}} = \sum^{N}_{k=1} E^{k}\]
Si cerca di minimizzare questo valore ragionando pattern-by-pattern, calcolando e minimizzando l’errore sulla singola istanza \(k\).
Self-Organizing Maps
SOM
Apprendimento non supervisionato
Strutture bidimensionali dove i neuroni sono disposti in una griglia.
- la griglia è solo una visualizzazione, non ci sono pesi tra i neuroni
- ogni neurone ha un suo vettore pesi \(w_{i}\) della stessa dimensione dell’input
- anche detti prototype vector, rappresentazioni associate al neurone
- qual’e' il tipo di stimolo che il neurone rappresenta
- l’input e' un vettore \(x\) di dimensione \(n\)
La best matching unit (BMU) e' il neurone attivato maggiormente dall’input
- corrisponde meglio allo stimolo
- attivazione e' il prodotto scalare \(x \cdot w_{i}\)
- questo e' anche il neurone con la minima distanza euclidea da \(x\)
- \[i: \forall j ||x - w_{i}|| \le ||x - w_{j}||\]
- se tutti i vettori hanno la stessa norma la minima distanza euclidea e il massimo prodotto scalare vanno di pari passo, se non e' cosi' viene considerata la distanza come definizione
Il learning va a modificare i pesi del BMU in modo da aumentare la probabilità che questo sia il neurone vincente per lo stesso input o simili.
- avviciniamo il vettore pesi di
BMUallo stimolo
Learning
Una forma di competitive learning
- una volta trovata la
BMUsi correggono i pesi - \[w_{i}(n+1) = w_{i}(n) + \eta(n)(x - w_{i}(n))\]
- dopo la correzione \(w_{i}\) è più simile a \(x\)
Il learning rate solitamente decresce con il procedere dell’apprendimento, il cambiamento in generale è regolato: \[\eta(n) = \]
Inoltre a ogni neurone \(i\) è assegnato un vicinato (neighberhood) cui è propagata la correzione dei pesi.
- una gaussiana che decresce con l’aumentare della distanza tra neuroni
- cooperazione tra i neuroni
\[w_{j} (n+1)= w_{j} (n) + \eta (n) h_{j,i} (n) (x - w_{j} (n))\] \[h_{j,i} (n) = \exp \Big (- \frac{d_{j,i}^2}{2\sigma (n)^2}\Big )\] \[\sigma (n) = \sigma _{0}\]
Ci sono 2 fasi, a grosso modo
- auto organization
- convergence
Topographic Error \[\text{TE} = \frac{1}{L} \sum_{l=1}^{L} u(x_{l})\]
Hopfield Networks
I Hopfield Networks sono una forma di rete neurale ricorrente, popolarizzata da John Hopfield nel 1982.
- ogni neurone è collegato a ogni altro tranne se stesso con pesi simmetrici
- la attivazione dei neuroni è calcolata in maniera asincrona
- scelta una unità la sua attività alpha viene calcolata dalle equazioni
\[v_j = \sum_{i=0}^{N} w_{ji}y_{i}(n)\]
\begin{align*}
\phi(v_{j})(n)=
\begin{cases}
1 \qquad &\text{if } v_j (n) >0\\
-1 \qquad &\text{if } v_j (n) <0\\
\phi(v_j)(n-1) \qquad &\text{if } v_j (n) =0
\end{cases}
\end{align*}
In queste configurazioni si possono raggiungere degli stati stabili, dove: \[\forall i, y_{i} (n+1) = y_{i}(n)\] In generale la negazione di uno stato stabile rimane stabile.
Si dimostra un teorema di convergenza per cui da un qualsiasi stato di partenza è garantito si raggiunge in un numero di passi finiti a uno stato stabile.
Le memorie fondamentali sono inserite all’interno della rete e questa imparerà a riconoscere versioni parziali/corrotte di queste sue memorie.
- la rete fa pattern completion
Il problema è:
- come individuare la configurazione di pesi cui corrispondono stati stabili le configurazioni di attivazioni delle memorie fondamentali
Storage
Le memorie fondamentali sono attrattori di versioni corrotte in input.
- il principio di Hebb per l’apprendimento ci aiuta nello storage
When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased. $cit
- fire together means strong connection
- i neuroni si rafforzano
Nella rete di Hopfield neuroni concordi avranno pesi tra loro positivi: si rafforzano. Generalizzando il principio vogliamo che neuroni che vogliamo opposti siano connessi da sinapsi negative.
In questa fase si decidono le memorie fondamentali
- le configurazioni di attivazione dei neuroni
Date queste vengono calcolati one-shot i pesi.
Data una singola memoria fondamentale è semplice: \[w_{ij} = f_{}_1(i) \times f_1(j)\]
- attivazioni discorde indeboliscono la connessione
Date \(M\) memorie fondamentali, \(f_1 \cdots f_{M}\) di dimensioni \(M\).
\begin{align*}
w_{ji} =
\begin{cases}
\frac{1}{M}\sum_{k=1}^{M} f_{k}(i) \times f_{k}(j) \qquad &j \neq i \\
0 &j = i
\end{cases}
\end{align*}
- questa regola funziona bene se abbiamo poche memorie fondamentali e non in conflitto
Retrieval
- Initialization
- si imposta la rete nello stato presentato \(x\)
- Iteration until convergence
- update degli elementi asincronicamente scegliendo unità random
\[v_j = \sum_{i=0}^{N} w_{ji}y_{i}(n)\]
\begin{align*}
\phi(v_{j})(n)=
\begin{cases}
1 \qquad &\text{if } v_j (n) >0\\
-1 \qquad &\text{if } v_j (n) <0\\
\phi(v_j)(n-1) \qquad &\text{if } v_j (n) =0
\end{cases}
\end{align*}
- Convergence to stable state
- Output
Convergence Theorem
Dato un qualsiasi stato iniziale la rete converge a uno stato stabile.
- non è più possibile modificare lo stato della rete attraverso la regola di aggiornamento
Il teorema si basa sul concetto di energia.
- energy is bad!
Una rete con alta energia è molto propensa a modifiche di stato, molto instabile. Al contrario una bassa energia indica una rete stabile.
- date \(N\) unità ci sono \(2^{N}\) possibili stati della rete
- a ogni stato si associa un livello di energia
- si prova che ogni cambiamento di stato porta a un abbassamento dell’energia
- c’è un momento in cui lo stato (stabile) non può più modificarsi in un altro stato
La definizione di energia: \[E = - \frac{1}{2} \sum_{i}\sum_{j}w_{ij} y_{i}y_{j}\]
- ogni prodotto interno è positivo con
- \(y\) concorde e \(w\) positivo
- \(y\) discorde e \(w\) negativo
- la sommatoria è negata, quindi coppie di neuroni per cui il prodotto e' positivo portano il livello di energia ad abbassarsi
\begin{align*} E = - \frac{1}{2} \sum_{i}\sum_{j}w_{ij} y_{i}y_{j} = - \frac{1}{2} \sum_{i}\sum_{j}w_{ij} y_{i}y_{j} \end{align*}
Qualities
- complete partial patterns
- generalize, given similar inputs to memory they recover the corresponding information
- fault tolerant, if synapses get broken the networks still works
- extraction of prototypes, a network learning similar information creates a prototype
- Hebb like
Drawbacks
- spurious states
- not all fundamental memories are stable states
- storage capacity with few errors given \(N\) units is \(0.14 N\)
Boltzmann Machines
Le Boltzmann Machines utilizzano la rete per costruire interpretazioni degli input sensoriali.
- input rappresentato dalle unità visibili
- interpretazione rappresentata dallo stato delle unità nascoste
- l’errore della interpretazione viene rappresentato dall’energia
- nascono dal problema degli stati spuri delle Hopfield Networks
- commettono errori e perciò andavano ridotte le capacita di memorizzazione
Hopfield, Feinstein e Palmer suggeriscono
- introdurre una fase di unlearning
- questo si libera di minimi spuri profondi
Crick e Mitchison proposero
- unlearning come funzione del sogno
- per questo non ci si ricorda dei sogni
Si cerca una funzione di costo da minimizzare per guidare questo unlearning
L’architettura della rete viene modificata
- la rete viene utilizzata per costruire interpretazioni dell’input sensoriale
- i neuroni sono divisi in
- livello visibile
- utilizzato per comunicare l’input
- livello nascosto
- trovano correlazioni di attivazione a livello visibile
- si allenano a riconoscere versioni corrotte di queste correlazioni
- ogni unità hidden si specializza a riconoscere una specifica feature dell’input da riconoscere e ricostruire a livello visible
- livello visibile
Nel caso delle Restricted Boltzmann Machines:
- tutti i neuroni visible sono connessi a tutti i neuroni hidden
- non ci sono connessioni tra i neuroni hidden
- non ci sono connessioni tra i neuroni visible
Le varie unità nascoste concorrono tra di loro per dare una interpretazione di un dato pattern visivo / input
- altre unità hidden possono eccitare a loro volta interpretazioni coerenti
- riconoscono o forzano configurazioni di input
Anche in queste reti migliore è l’interpretazione minore è l’energia della rete.
- la regola di cambiamento di stato impone di minimizzare sempre l’energia
- rende impossibile superare minimi locali e trovare i minimi globali desiderati
Questo limite si supera utilizzando una regola stocastica di update al posto di quella deterministica della rete di Hopfield.
- si utilizzano unità stocastiche biased
\[p(s_{i}=1)=\frac{1}{1+e^{-\Delta E_i /T}}\]
- probabilità che il neurone \(i\) abbia attivazione 1
- \(\Delta E_i = E(s_i = 0 ) - E(s_i = 1)\)
- se l’energia peggiora la \(p\) risultante sarà minore di 0.5
- se l’energia migliora la \(p\) risultante sarà maggiore di 0.5
- \(T\) è la temperatura, ammontare di rumore
- temperature maggiori portano grossi cambiamenti di stato
- temperature basse portano pochi cambiamenti, comportamento più deterministico e simile alle reti di Hopfield
- Hilton suggerisce temperature alte, supponiamo sempre 1
- inizialmente veniva utilizzata diminuendo mano a mano la temperatura con il trascorrere dell’apprendimento
\[E=-\sum w_{kj} s_{k}s_{j} - \sum s_{k}b_{k}\quad \forall k,j\]
- le
BMsono modelli generativi, apprendono a riprodurre a livello visibile ilTS- l’apprendimento vuole massimizzare il prodotto delle probabilità assegnate dalla
BMai vettori binari nelTS - si procede calcolando le probabilità assegnate con il
TSe facendo sampling in base a queste probabilità - si arriva a una fantasy che la
BMtende a generare
- l’apprendimento vuole massimizzare il prodotto delle probabilità assegnate dalla
Restricted Boltzmann Machines
RBM
Reference: A Practical Guide to Training Restricted Boltzmann Machines
- ogni neurone hidden è connesso a ogni neurone visible
- i neuroni hidden non sono connessi ad altri neuroni hidden
- i neuroni visible non sono connessi ad altri neuroni visible
In fase di training si presentano input in livello visible e si modificano le attivazioni della rete hidden, non più in maniera deterministica ma stocastica.
- in base a temperatura e energy gap
- anche se assecondando Hilton la temperatura viene ignorata impostandola sempre a 1
- sfuggendo a minimi locali di energia
Nel calcolo del energy gap tutti i termini non contenenti \(i\) sono eliminati in quanto identici nei casi \(s_{i} = 0, s_{i} = 1\). \[\Delta E_{i} = \Sum w_{ij} s_{i} + b_{i} \quad \forall j\]
Contrastive Divergence
Algoritmo di apprendimento basato su solamente due passaggi tra livello visible e hidden.
- A very surprising short-cut
Correzione della discrepanza tra dato e ricostruzione della rete in due passi.
- quindi tra l’elemento del
TSpresentato e la ricostruzione successiva a livello visible fatta dalla rete addestrata
I passaggi sono:
- data → hidden → reconstruction → hidden
\[\Delta w_{ij} = \eta (\lang v_{i} h_{j} \rang^{0} - \lang v_{i} h_{j} \rang^{1}) \] Quindi i prodotti di attivazione presi a \(t=0\) e \(t=1\).
- \(v\) sta per visible, \(h\) sta per hidden
- momento di clamping del training pattern a livello visible
- momento di recostruction a livello visible
- può essere diversa da quella presentata inizialmente: una fantasy della rete che l’algoritmo mira a correggere
L’idea è che ci si accorge che alla rete piace divagare rispetto al TS dopo solo due passi, è inutile lasciare che la rete del genere si stabilizzi in quanto non genererà i pattern desiderati.
Ogni neurone riconosce una feature specifica.
Deep Neural Networks w/ RBMs
DNN
Steps to learning:
- raw input vector representation
- slightly higher level representation
- …
- very high level representation
Il passaggio da questi step è necessario in quanto non è possibile passare da pixel a concetti astratti. È più semplice passare tra astrazioni intermedie: features.
L’obiettivo dei DNN è di attraversare tutti questi livelli di astrazione.
Il meccanismo del learning è analogo a quello delle RBM, solamente applicato a più livelli.
Più la rete è profonda più la rete è efficace a riconoscere l’input ma è più difficile da allenare, in quanto ci sono molti minimi locali. In queste reti per risolvere questo problema si utilizza il pre-training:
- non inizializzare i pesi della rete profonda casualmente ma utilizzando le
RBM
L’implementazione può essere fatta:
- auto-associators
- non supervisionati
- imparano tramite backpropagation a riprodurre in output l’input stesso
- si pongono vincoli ai neuroni hidden, in particolare si impone una attivazione sparsa in modo che non impari una funzione identità triviale
- l’ultimo livello viene dato in input a un livello supervisionato trattato poi con i criteri supervisionati
- Stacked
RBMs- hanno un focus generativo
- To recognize shapes, first learn to generate images[
$cit Hinton] - prima si addestra il primo livello che riconosce i pixel
- li genera a livello visible
- poi si addestra un secondo livello basato sulle attivazioni nel livello hidden precedentemente addestrato
- genera questo livello hidden a livello visible
- si procede incrementalmente in questo modo
- si prova che ogni volta che si aggiunge un layer di features che le performance della rete migliora
Si può fare fine-tuning di queste pile di RBM utilizzando la backpropagation
Oppure utilizzando Deep Autoencoders si può comprimere l’informazione livello dopo livello
- questo è ottenuto impilando
RBM - pretraining
- si passa a
RMBsempre più piccole a riconoscere i pattern di attivazione imparati a livello precedente - qui si fa il grosso del lavoro nell’apprendimento dei pesi
- si passa a
- unrolling
- si fa l’operazione inversa da informazione codificata fino a dimensione originale
- fine-tuning
- i pesi sono rifiniti in maniera supervisionata per migliorare l’output finale
- non cambia più di molto i pesi
Deep Belief Networks
DBN
Impara a generare a livello visible elementi del TS.
Si combinano due RBM impilandole e rimuovendo i pesi che passavano da livello visible a livello hidden, i pesi in risalita di tutte le RBM tranne quella top.
- solo pesi discendenti a livello più basso
- non è più una
RBM
- non è più una
Si parte a livello top da una configurazione iniziale casuale si continua fino a che non si raggiunge una configurazione stabile o di equilibrio termico, una volta raggiunta si propaga la configurazione a livello bottom generando una configurazione.
Fasi:
- wake propaga l’attivazione dall’basso verso l’alto
- si correggono i pesi a scendere ogni volta per aumentare la probabilità che l’input venga riprodotto
- sleep
- fase di fine-tuning
- a partire dalle configurazioni delle
RBMsovrastanti si correggono i pesi a salire - il nome è questo in quanto in questo passaggio le
RBMproducono le fantasy che preferiscono
Supervised Learning
Dati di apprendimento sono etichettati.
Single Layer feed-forward
Perceptron
Non ci sono neuroni nascosti.
Multi Layer feed-forward
Input Layer → Hidden Layer → Output Layer
Può essere completamente (ogni neurone è connesso a ognuno dei precedenti) o parzialmente connesso.
- le unità nascoste estraggono dinamiche di livello superiore
Tratta dati non linearmente separabili.
L’algoritmo di back-propagation minimizza l’errore con la tecnica della discesa del gradiente
- per questo la funzione associata al percettrone deve essere derivabile
Una tipica funzione di attivazione è la sigmoide
\[\phi(v_{j}) = \frac{1}{1+e^{-av_{j}}}\]
con \(a > 0\)
\[v_{j} = \sum w_{ji}y_{i}\] dove \(y_{i}\) è l’output del neurone \(i\)
\(\phi\) si avvicina alla funzione gradino (step) al crescere di \(a\).
Backpropagation Algorithm
Cerca pesi che minimizzano l’errore totale della rete sul Training Set.
Consiste nella applicazione ripetuta di 2 passi:
- forward pass, la rete viene attivata con un esempio e si calcola l’errore di ogni neurone di output
- backward pass, l’errore di rete è utilizzato per aggiornare i pesi
Il processo è più complesso che per Adaline in quanto i nodi nascosti contribuiscono all’errore.
Partendo dall’output layer l’errore viene propagato all’indietro attraverso la rete (layer by layer), calcolando ricorsivamente il gradiente locale di ogni peso.
Calcoliamo l’errore partendo dal layer di output, al \(n\)-esimo training example:
\begin{align*}
e_{j} (n) &= d_{j}(n) - y_{j}(n) \\
E(n) &= \frac{1}{2} \sum e_{j}^{2} (n) \\
E_{}_{AV} &= \frac{1}{N}\sum^{N}_{n=1} E(n)
\end{align*}
Aggiornamento dei pesi:
\begin{align*}
w_{ji} &= w_{ji} + \Delta w_{ji} \\
\Delta w_{ji} &= - \eta \frac{\delta E}{\delta w_{ji}} \quad \eta > 0\
\end{align*}
- il delta viene corretto nella direzione opposta del gradiente di \(E\)
- il gradiente è l’insieme di tutte le derivate di \(E\) in funzione dei pesi
- queste sono tante quante i pesi, ogni variazione di peso ha un impatto sull’errore totale della rete
- il gradiente è l’insieme di tutte le derivate di \(E\) in funzione dei pesi
-
Caso del neurone di output
In questo caso il neurone \(j\) è a conoscenza del suo errore e può andare a modificare gli input dei neuroni del livello successivo.
\[-\frac{\delta E}{\delta v_{j}} = - \frac{\delta E}{\delta e_{j}}\frac{\delta e_{j}}{\delta y_{j}}\frac{\delta y_{j}}{\delta v_{j}} = - e_{j}(-1)\phi' (v_{j}) = \delta_j\]
\[\Delta w_{ji} = \eta e_{j} \phi' (v_{j})y_{i}\]
-
Caso del neurone hidden
Con \(j\) neurone hidden: \[\Delta w_{ji} = \eta \delta_j y_{i}\] \[\delta_{j} = \phi' (v_{j}) \sum_{k} \delta_{k}w_{kj}\]
-
Delta Rule
\begin{align*} w_{ji} &= w_{ij} + \Delta w_{ji} \\
\Delta w_{ji} &= \eta \delta_{j} y_{i} \end{align*}con
\begin{align*} \delta_j = \begin{cases} \phi'(v_j)(d_j - y_j) \qquad j \text{ neurone di output}\\
\phi'(v_j) \sum_{k} \delta_{k} w_{kj}\qquad j \text{ neurone hidden} \end{cases} \end{align*}con \[\phi' (v_{j}) = \alpha v_{j}(1-v_{j})\]
Radial-Basis Function Neural Network
RBF - Radial Basis Function Network
Una funzione radiale restituisce un output dipendente dalla distanza di input e un vettore interno. Una tipologia di RBF molto diffuse sono le Gaussiane.
- se il problema lo consente le
RBFpossono delimitare più facilmente aree con meno neuroni - le architetture basate su
RBFsono solitamente con un unico livello nascosto, con \(m_1\) funzioni radiali- \(m\) input
- le funzioni di attivazione
RBFsono utilizzate nel livello hidden- il livello di uscita è lineare
\[\phi_{}_{1} \cdots \phi_{k}\] \[y = w_{1}\phi_{1} (||x - t_{1}||) + \dots + w_{m_{1}}\phi_{m_{1}}(||x - t_{m_{1}}||)\]
- il centro della funzione radiale è \(t\)
- un generico centro \(t_k\) ha \(m\) componenti1
- le componenti dei centri fanno le veci dei pesi del neurone hidden del multilayer perceptron
- un altro iperparametro è lo spread \(\sigma\)
- indica quanto la funzione sia aperta o chiusa
- spread grande significa proiezioni (circonferenze) grandi
- tutti i neuroni nascosti diventano sensibili a input vicini al loro centro
- la sensibilità dei neuroni può essere aggiustato tramite lo spread \(\sigma\), grande significa meno sensibile
I pesi dell’uscita \(y\) individuano il decision boundary nel nuovo spazio \(\phi\)
- questo in quanto il problema - precedentemente non linearmente separabile - viene trasposto in un nuovo spazio dalle \(\phi\) in cui è linearmente separabile
Si cerca una funzione \(F: R^m \Rightarrow R\) che le condizioni di interpolazione \(F(x_i) = d_i\) Si cercano i pesi che definiscano \(F(x)\)
- per questo si passa attraverso pseudo-inversione matriciale
Interpolation
\(\{x_i \in R^{m} , i = 1 \cdots N\}\) set di punti \(\{d_i \in R , i = 1 \cdots N\}\) set numeri reali Cerchiamo una funzione \(F: R^m \Rightarrow R\) Condizione di interpolazione: \[F(x_i) = d_{i}\] Si deriva dalla definizione di \(F(x)\) il risultato del calcolo sulla matrice \(N\) \[\Phi w = d\]
- \(\Phi\) matrice quadrata delle \(\phi\)
- come se prendessimo come centri radiali tutte gli esempi \(x_{}_i\)
- nell’uso concreto i centri saranno meno
- \(w\) vettore delle \(w_i\)
- \(d\) vettore delle \(d_i\)
\(\Phi\) è una matrice quadrata in quanto tutti gli \(i\) input vengono utilizzati per ogni riga come centro della RBF
Definita la pseudo-inversa \[\Phi^{+}= (\Phi^{T}\Phi)^{-1}\Phi^{T}\]
I pesi si trovano risolvendo il sistema lineare
\[w^T = \Phi^+ d^T\]
L’algoritmo schematicamente allora consiste in tre passi:
- scegli i centri casualmente
- calcola la spread della funzione
RBFcon la tecnica di normalizzazione - trova i pesi utilizzando il metodo di pseudo-inversione
Extreme Learning Machine
ELM
Extreme learning machine: Theory and applications
\(\text{Theorem 2.1} \quad\) Given a standard
SLFNwith \(N\) hidden nodes and activation function \(g: R\to R\) which is infinitely differentiable in any interval, for \(N\) arbitrary distinct samples \((x_{i},t_{i})\), where \(x_{i}\in R^{n}\) and \(t_{i} \in R^{m}\), for any \(w_{i}\) and \(b_{i}\) randomly chosen from any intervals of \(R^{n}\) and \(R\), respectively, according to any continuous probability distribution, then with probability one, the hidden layer output matrix \(H\) of theSLFNis invertible and \(|| H\beta - T || = 0\).
\(\text{Theorem 2.2} \quad\) Given any small positive value \(\epsilon > 0\) and activation function \(g: R\to R\) which is infinitely differentiable in any interval, there exists \(\tilde{N} \le N\) such that for \(N\) arbitrary distinct samples \((x_{i},t_{i})\), where \(x_{i}\in R^{n}\) and \(t_{i} \in R^{m}\), for any \(w_{i}\) and \(b_{i}\) randomly chosen from any intervals of \(R^{n}\) and \(R\), respectively, according to any continuous probability distribution, then with probability one, \(|| H_{N \times \tilde{N}} \beta_{\tilde{N}\times m} - T_{N\times m} || < 0\).
Piu' piccola e' la norma dei pesi migliori sono le performance della generalizzazione, tendenzialmente.
- per questo l’algoritmo proposto tende a buone prestazioni per
FFNN
Recurrent Neural Networks
RNN
Il learning è supervisionato. Si trattano sequenze di dati, si cerca di produrre qualcosa.
- una traduzione di qualche tipo
- speech recognition
- machine translation
- music generation
- sentiment classification
- video activity recognition
- un informazione mancante
- DNA sequence analysis
- name entity recognition
- predict whether a verb is singular or plural
- learn language model, predict next word
- grammaticality of a sentence
Generalmente si utilizzano queste reti per task di Natural Language Generation.
- \(x(i)^{
}\) per considerare l’elemento t-esimo della sequenza \(i\) - \(y(i)^{
}\) per considerare il t-esimo output della sequenza dell’esempio \(i\) - \(Tx(i)\) lunghezza della sequenza \(x(i)\)
- \(Ty(i)\) può avere dimensione diversa
NB: diversamente dalle reti FF la lunghezza dell’input non è fissata.
Le parole del vocabolario hanno una rappresentazione one-hot
- codificate con dei bit
- un vettore di dimensione \(N\) uguale alla lunghezza del
TSe l’unico bit a 1 quello corrispondente alla posizione della parola considerata nel vocabolario
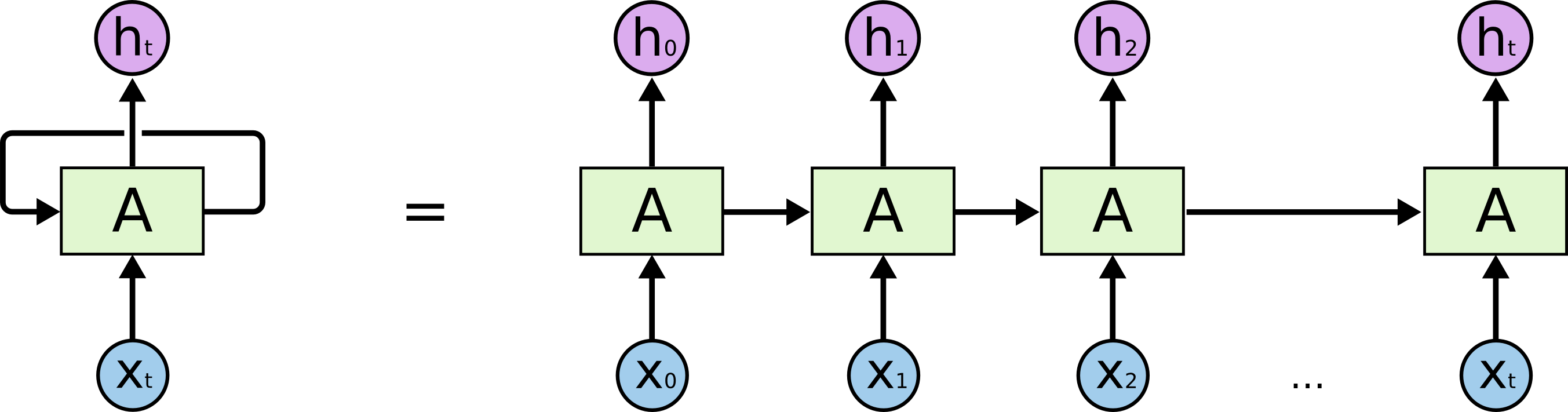
Figure 1: RNN rolled e unrolled
I motivi per cui vengono utilizzate queste reti e non quelle standard FF:
- input e output possono avere lunghezze diverse
- condivide feature imparate in diverse posizioni del testo
- in reti
FFnon c’è corrispondenza tra parole uguali in posizioni diverse, questi sarebbero stimoli completamente diverse
- in reti
- tengono conto del contesto, fondamentale in compiti di traduzione
- considera la storia dell’input, ciò che ha incontrato nel tempo precedente
Dato che le lunghezze di input e output possono essere diverse esistono diverse relazioni tra queste:
- one to one
- image classification
- one to many
- image captioning
- music generation
- many to one
- sentiment analysis
- many to many (non allineato)
- translation
- many to many (allineato, dà l’output \(n\) subito dopo la presentazione dell’input \(n\))
- frame by frame video classification
Oltre all’input previsto per il passo \(t\) viene considerato anche l’output a livello hidden al passo \(t-1\).
\begin{align*}
a^{<0>} &= \overline 0 \\
a^{<1>} &= g(w_{aa} a^{<0>} + w_{ax} x^{<1>} + b_{a}) \\
\overline y^{<1>} &= g(w_{ya} a^{<1>} + b_{y})
\end{align*}
I pesi sono imparati nel corso dell’apprendimento per minimizzare le loss function. I pesi sono gli stessi nei vari passi \(t\).
\[L^{
L’apprendimento avviene anche in questo caso per backpropagation, in questo caso un particolare tipo chiamato Backpropagation Through Time.
BPTT- il nome viene dal fatto che la propagazione passa all’indietro attraverso i passi temporali della rete
La BPTT ha il problema tecnico della scomparsa o l’esplosione del gradiente
- vanishing or exploding gradient
Le vanilla RNN cells contengono una tangente iperbolica:
\[h_{t} = tanh (W h_{t} + UX_{t}+b ) \]
Questa funzione trasporta informazione nella sua parte centrale (derivate diverse da 0).
Long Short Term Memory
LSTM
Blog a Riguardo
- cattura dipendenze long distance, una memoria
- le unità hanno dei gate che decidono quando aggiornare le celle di memoria, cosa mantenere e cosa dimenticare[
/refresh when new subject/] - forget gate, moltiplicato elemento per elemento per \(C\)
- ogni bit indica se mantenere o dimenticare
- input gate
- questo è moltiplicato allo stato candidato della cella e poi aggiunto alla memoria
- output gate
- computato con input, hidden state passato e memoria corrente
- forget gate, moltiplicato elemento per elemento per \(C\)
- queste celle di memoria sostituiscono le unità hidden di una normale
RNN
Lo stato della cella \(C\) è rappresentata orizzontalmente nei diagrammi, trasporta informazioni attraverso l’intera catena, interagendo con le unità che incontra.
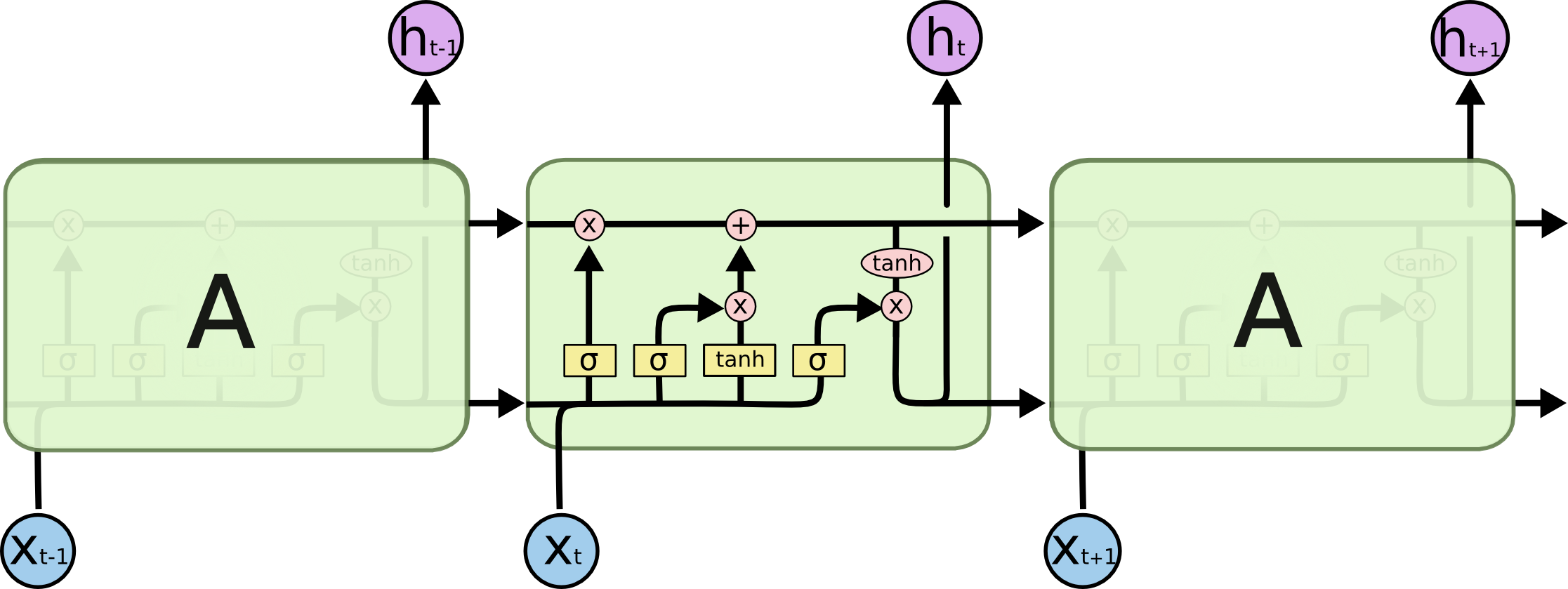
I gate restituiscono vettori di bit della dimensione della memoria LSTM \(C_{t-1}\).
\begin{align*}
f_t &= \sigma (W_f \cdot [h_{t-1}, x_{t}] + b_f)\\
i_{t} &= \sigma (W_{i} \cdot [h_{t-1},x_t ]+ b_{i})\\
\tilde C_{t} &= \text{tanh}(W_{C} \cdot [h_{t-1}, x_{t}] + b_{C})\\
o_{t} &= \sigma (W_{o} \cdot [h_{t-1},x_t ]+ b_{o})\\
h_{t} &= o_{t} \times \text{tanh}(C_{t})
\end{align*}
Lo scopo dello stato della cella di fornire un informazione stabile che non si annulli a causa dei vanishing gradient. L’output è detto hidden state.
Gated Recurrent Unit
GRU
Un tentativo di semplificare le LSTM del 2014.
\begin{align*}
z_t &= \sigma (W_z \cdot [h_{t-1} ,x_t])\\
r_t &= \sigma (W_r \cdot [h_{t-1}, x_t])\\
\tilde h_t &= tanh (W\cdot [r_t \cdot h_{t-1}, x_t])\\
h_t &= (1-z_t)\cdot h_{t-1} + z_t \cdot \tilde h_t
\end{align*}
Encoder-Decoder
Architettura di RNN in cui la prima parte processa l’input e la seconda genera l’output.
- encoder
- l’output delle celle viene scartato
- lo stato (hidden e non) dell’ultima cella viene inserito in un summary vector[
L’ultima cella è quella che ha visto tutto l’input.]
- decoder
- prende in input il summary vector
- produce la traduzione
- Teacher forcing - training
- il primo input è un token di
START - successivamente in input si da l’output atteso
- il primo input è un token di
- Autoregressive generation - generazione
- il primo input è un token di
START - poi a catena si danno in input gli output precedenti
- si procede fino a un token di
END
- il primo input è un token di
Il processo di passaggio da hidden state a token finale è composto da:
- lo stato passa per una trasformazione lineare
- si ottiene un vettore di dimensione del vocabolario chiamato logits
- si fa una softmax sulla logits ottenendo il logaritmo di una distribuzione di probabilità sul vocabolario
- chiamata log_probs
Il problema di una architettura del genere è che in frasi molto lunghe il summary vector deve riuscire a codificare tutta l’informazione, andando a perdere molta dell’informazione prodotta all’inizio della catena. La soluzione a questo problema è quello di avere diversi vettori di questo tipo che codifichino intervalli di tempo diversi del flusso dati. Questa tecnica è chiamata attention. Il decoder utilizza l’attenzione ad ogni time step utilizzando gli hidden state del encoder al time step relativo.
- si confrontano questi hidden state nella finestra temporale con il decoder hidden state, si attribuiscono score più alti a stati più simili. A questi attention score si applica una softmax ottenendo una distribuzione di probabilità
- ogni vettore è moltiplicato per il proprio softmaxed-score
- questi vettori sono sommati producendo il context vector per il decoder al time step
Questo context vector viene concatenato con l’output della cella decoder e questo viene trasformato per selezionare la parola del dizionario generata.
\begin{align*}
C_i &= \sum_{j=1}^{T_x} a_{ij}h_j \\
a_{ij} &= \frac{\exp (e_{ij})}{\sum_{k=1}^{T_x} \exp (e_{jk})} \\
e_{ij} &= \lang W_a s_{i-1}, U_a h_j\rang
\end{align*}
- \(a\) sono gli attention score
- \(C\) è il contesto che viene preso in input dalla cella decoder
Transformer
- Contributed by (Vaswani et al. 2017)
- Step-By-Step Breakdown
- stato dell’arte

Il modello si basa sulla tecnica della self attention.
- l’attenzione va da input a input, per questo il self
L’attention score non è altro che il dot product tra vettori query e keys, che calcola quanto due matrici si somigliano.
- spesso le parole pongono l’attenzione su se stesse, in casi particolari però non è così
\begin{align*} \text{Attention}(Q,K,V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V \end{align*}
Questo meccanismo di attention viene applicato più volte: Multi-head attention. Il modello nasce con 8 di queste teste. Ogni attention head ha le sue tre matrici \(W^{Q},W^{K},W^{V}\).
- inizializzate random, poi imparate durante il training
- l’idea è che ogni head si specializzerà su una specifica feature del linguaggio
- una maniera per aumentare la dimensione del transformer, oltre a renderlo più profondo
Gli output \(Z_{i}\) delle head vengono concatenate tra loro e processate da un layer feed-forward con pesi imparati \(W^{O}\). Si ottiene una matrice \(Z\) finale della dimensione corretta, uguale alla dimensione dell’input \(X\).
Un limite dell’architettura fin’ora è che non è in grado di processare l’ordine delle singole parole in input. Questo è risolto tramite positional encoding. Viene sommato a ogni input il proprio vettore di positional encoding.
- questi \(PE\) sono derivate da funzioni di seno e coseno
\begin{align*}
PE(pos, 2i) &= \sin (pos / 10000^{2i/d_{model})})\\
PE(pos, 2i+1) &= \cos (pos / 10000^{2i/d_{model})})
\end{align*}
Questi embedding possono anche essere semplicemente imparati dal modello e non essere hard-coded.
Unsupervised Learning
In questa categoria si collocano le Reti Neurali Profonde:
- organizzano i propri livelli gerarchicamente
- selezione delle feature più importanti a scapito di quelle ignorabili
- unsupervised feature learning
- le caratteristiche dei dati che permettano la risoluzione del problema sono trovate in maniera automatica
- non serve pre-precessing da parte di esperti sui dati
- representation learning
La complessità di una rete è determinata da:
- profondità
- numero delle connessioni tra i neuroni
- numero di pesi diversi tra i neuroni
Convolutional Neural Network
CNN
Molto utilizzate per lavorare su immagini.
- processamento locale
- i neuroni di un certo livello sono connessi ad altri neuroni del livello precedente solo localmente
- riduzione del numero delle connessioni
- specializzazioni dei neuroni su una zona dell’input
- parti diverse della rete si occupano di compiti diversi
Il livello convolutivo lavora come un filtro, processando i valori del livello precedente. Il processo procede per stride man mano applicando il filtro.
- lo stride individua di quanto si sposta la finestra passo dopo passo
- per evitare che la finestra fuoriesca dalla matrice si aggiunge del padding della grandezza giusta
Solitamente si utilizzano rete neurali multi-dimensionali:
- ogni livello di neuroni viene chiamato feature map
- una particolare mappa apprende una particolare feature dell’input
- sia input che output hanno multiple feature map
- diverse feature map insieme compongono un tensore
Un livello di neuroni si occupa di un task di compressione dell’informazione chiamato pooling (downsampling)
- questo task genera delle feature map di dimensioni minori
- l’aggregazione dell’informazione può avvenire utilizzando max-pooling o average-pooling
Le immagini sono rappresentate ma matrici numeriche
- di 3 canali se a colori
- questo tipo di oggetti sono conosciuti come tensori, che possono avere anche più di 3 dimensioni
Image classification using MLP
L’immagine deve essere appiattita. Non l’ideale:
- viene persa informazione posizionale
- ogni pixel è una feature (ridondante)
- troppi parametri
- questo porta a overfitting
Il problema è che l’input di cui ha bisogno una MLP è una serie di feature molto più significative dei pixel di cui è composta l’immagine.
Serve una feature map.
Convolution
Per ottenere una feature map viene utilizzata la convoluzione. Si usano kernel ovvero piccole matrici di pesi (anche chiamati filter).
- questi passano l’input matrix calcolando la feature map
- ogni elemento della feature map è una somma pesata locale che utilizza i pesi del filtro
-
Proprietà
- pesi sparsi
- i calcoli sono più veloci e localizzati
- i parametri sono condivisi
- l’analisi è locale
- equivarianza rispetto la traslazione
- se la feature è in zone diverse nella mappa non ha importanza
- stessi pesi significa che i neuroni di quella zona stanno cercando la stessa feature
- pesi sparsi
Filtri
Definiti da esperti:
- identity
- edge detection
- sharpen
- gaussian blur
Ora i CNN imparano in base al task definito i filtri migliori per risolverlo.
-
Iperparametri
- numero di filtri
- kernel size
- quanto l’analisi è locale
- un kernel grande come l’input si torna al percettrone
- padding
- se le parti periferiche sono importanti per l’analisi si aggiunge un padding, solitamente inizializzati a 0
- stride
- dimensione dal salto fatto dal kernel a ogni passo
- se uguale alla dimensione del kernel si perde la caratteristica della convoluzione in quanto ogni pixel è considerato una sola volta
Pooling
Molti valori della feature map sono comunque inutili. Il pooling:
- riduce la dimensionalità
- seleziona i valori più informativi
- invariante su piccole traslazioni
- in quanto solitamente si usa max che non dipende dall’ordine
- non ha pesi
I possibili pooling sono solitamente
- average
- max
-
Iperparametri
- kernel size (2x2)
- padding
- stride (2)
Convolutional Blocks
Blocchi composti da:
- convolution
- pooling layer
- activation function
- per evitare il vanishing gradient nelle reti molto profonde viene utilizzata
RELU
- per evitare il vanishing gradient nelle reti molto profonde viene utilizzata
Alla fine vengono estratta la feature map.
Questa (flattened) viene seguita da uno o più strati completamente connessi (MLP).[
RELU
REctified Linear Unit
\[f(u) = \max (0, u)\]
- funzione non derivabile
- derivata 0 per valori negativi
- derivata 1 per valori positivi
Questa funzione porta a una attivazione sparsa, dove non tutti i neuroni vengono attivati portando alcune componenti del gradiente a 0.
- questo permette pruning automatico
- nelle reti si tende ad abbondare con il numero di neuroni o di livelli necessari al problema
- in questo modo la rete può annullare delle componenti a piacimento durante il training
Pruning
In ambito industriale soprattutto, ma non solo, negli anni si è visto un aumento importante del numero dei parametri delle reti neurali. Per questo è stato necessario sviluppare delle buone tecniche di pruning per ovviare a questo problema.
NB architetture con un grande numero di parametri non hanno necessariamente un’accuratezza più alta.
Per pruning si intende una decrescita delle dimensioni di una rete neurale tramite l’eliminazione di parametri mantenendo performance accettabili. Si può distinguere in:
- pruning strutturato
- modifica anche la struttura stessa della rete eliminando neuroni interi (tutti i suoi archi uscenti sono annullati)
- non completamente esplorato in letteratura
- pruning non strutturato
- molto esplorato in letteratura
Entrambi portano alla riduzione dello spazio richiesto dalla rete.
Si osserva che questo processo di pruning avviene anche a livello biologico:
- le sinapsi degli infanti aumentano fino a 7-8 anni
- le sinapsi dei bambini di 15 sono diminuite rispetto a quel picco
- tuttavia le capacità di apprendimento continuano a migliorare
- questo suggerisce che biologicamente un numero minore ma gestite meglio di sinapsi è preferibile
Tecniche di Regolazione
Funzione di Loss: \[L (\Theta)=L(\Theta) + \lambda F(\Theta)\]
- coefficiente di regolarizzazione λ
- L1 regularization \[P(\Theta)=\sum_{n,i,j}|w^{n}_{i,j}|\]
- più efficace ma può essere complessa da applicare
- L2 regularization \[P(\Theta)=\sum_{n,i,j}|w^{n}_{i,j}|^{2}\]
La sola riduzione della norma dei pesi non è sufficiente ad effettuare pruning. Questo perché i pesi potrebbero non raggiungere lo 0.
Per fare questo viene deciso un threshold sotto il quale i pesi vengono annullati.
I pesi che desideriamo eliminare sono i pesi ridondanti nella rete. Per individuare questi parametri ci sono diverse tecniche.
Sensitivity
\[\Delta y \simeq \Delta w_{i} \frac{\delta y_{k}}{\delta w_{i}}\]
\[ S(y,w_{i})= \sum_{k=1}^{C}\alpha_{k}\big |\frac{\delta y_{k}}{\delta w_{i}}\big|\]
- \(C\) è la dimensione dell’output
- \(\alpha_{k}\) è un fattore scalare dei pesi
Ci interessano i parametri per cui la rete ha poca sensibilità, definiamo la insensitivity: \[\overline S(y,w_{i})= 1 - S(y,w_{i})\] Per garantire che questa sia sempre positiva: \[\overline S_{b}(y,w_{i})= \max [0, \overline S(y,w_{i})]\]
I pesi con derivata piccola devono essere ridotti e possibilmente eliminati.
Questa viene tenuta di conto nell’update dei pesi: \[w_{i}^{t} := w_{i}^{t-1} - \eta \frac{\delta L}{\delta w_{i}^{t-1}} - \lambda w_{i}^{t-1} \overline S_{b}(\sigma, w_{i}^{t-1})\]
Quindi se la sensitivity è alta (\(\overline S = 0\)) l’ultimo membro si annulla e non influenza l’update. Viceversa con insensitivity alta questo influenza l’update contribuendo a diminuire il peso.
Sviluppando questa idea si va a valutare direttamente la sensibilità a partire dalla variazione della loss: \[S(L,w_{i})= \frac{1}{C} \sum_{k=1}^{C} \Big | \frac{\delta L}{\delta y_{L,k}}\Big| \cdot \Big | \frac{\delta y_{i,k}}{\delta w_{i}}\Big |\] Approssimabile a: \[S(L,w_{i})= \Big | \frac{\delta L}{\delta w_{i}} \Big |\]
Irrelevance
Invece di modificare l’update dei pesi modificare la loss che si vada a minimizzare secondo un coefficiente di irrilevanza.
Si utilizza un esponenziale negativo, in questo modo asintoticamente questo tenderà a 0 con l’aumentare della derivata della loss rispetto al peso. Vale a dire che all’aumentare della derivata (parametro importante) diminuisce il parametro di irrelevance.
Questo parametro è definito: \[I_{n,i,j}= \exp \Big(- \frac{\delta L(\oveline w)}{\delta w_{i,j}^{n}}\Big) \qquad 0 < I_{n,i,j} < 1\]
Ridefiniamo la loss: \[L (\overline w ) = L(\overline w) + \lambda \sum_{n,i,j} \big ( I_{n,i,j} \cdot | w_{i,j}^{n}|^{2} \big)\]
Questo permette un metodo più generale che consente anche l’uso di altri ottimizzatori.
-
deve essere compatibile con l’input \(x_k\) per poter effettuare la distanza. ↩︎