Sistemi Intelligenti

• Professoressa: Cristina Baroglio
• PDF Version

Terminologia

• AI coniato da John McCarthy
• Dato, simbolo grezzo
• Informazione, un dato elaborato
• Conoscenza, campo di informazioni correlate tra loro
• Automazione
• Autonomi

Automazione

Campo in cui l’informatica più in generale viene applicata

• automazione del calcolo
• automazione contabile
• automazione della ricerca di informazione, motori di ricerca

Tratta di programmare un supporto a fare ogni passo, applicabile in domini fortemente ripetitivi

Autonomia

Svolta da un agente artificiale che risolve un compito

• non viene indicato passo passi il modo per raggiungere l’obiettivo
• vengono forniti solo compiti ad alto livello

Utile nei problemi:

• non deterministici
• in cui c’è molteplicità di soluzioni
• con dati di natura simbolica
• si ha una conoscenza ampia e completa
• dove l’informazione é parzialmente strutturata

Comprensione

Output attesi \(\implies\) comprensione? John R. Searle

Test di Turing

• test per definire se un computer é intelligente, o se un programma lo é
  • in linguaggio naturale
• per T lo é quando inganna l’uomo, imitando il comportamento umano
• un computer che deve passare il test non eseguirà gli ordini direttamente, in quanto questi vanno filtrati rispetto alle capacita di un umano
• The Imitation Game

Captcha

Completely Automated Public Turing-test to tell Computers and Humans Apart Turing test inverso

Strong & Weak

1. studio del pensiero e del comportamento umano, scienze cognitive
   • riprodurre l’intelligenza umana
2. risolvere problemi che richiederebbero intelligenza degli umani per essere risolto
   • non ci importa come l’umano ragiona, importa come risolvere il problema
   • task-oriented

Agente - Environment

L’agente é immerso in un ambiente e svolge in ciclo esecutivo:

1. Percepisce
2. Delibera
3. Agisce

L’ambiente definisce cosa e' efficace e cosa non lo e'. questo in base agli attuatori degli agenti possono essere posti in questo ambiente. L’ambiente, in base a come si evolve nel tempo della percezione e deliberazione, può essere:

• statico
• dinamico

Inoltre si può distinguere un ambiente:

• deterministico
  • possibile prevedere in che stato un azione sposta l’ambiente
• stocastico
  • non e' possibile prevedere in tutti i casi lo stato in cui ci si troverà dopo un azione

Agente Autonomo

• ha capacita di azione
• riceve compiti ad alto livello
• esplora alternative, numero esponenziale di possibilità da esplorare
• riconosce
  • se una strada non può portare a una soluzione
  • un strada già esplorata

Un AA rimane un programma, non farà ciò che non é programmato a fare

Il cuore dell’agente é la funzione deliberativa

• un agente é razionale se opera per conseguire il successo
• questo é possibile con una misura di prestazione utilizzata come guida

La razionalità ottimizza il risultato atteso

• possono intercorrere fattori ignoti o imprevedibili

Paradigma Dichiarativo

• imperativo: how, sequenza di passi
• dichiarativo: what, si sfrutta una knowledge base
  • il cuore é il Modulo dichiarativo che utilizza l’informazione dalla percezione e la propria knowledge base

Quindi:

• un programma, risolutore, produce un altro programma che risolva una particolare istanza del mondo

Risoluzione Automatica

• nella realtà di riferimento si astrae utilizzando degli stati
  • astraendo si lascia solo una descrizione essenziale
  • discreti
  • tra questi ci saranno stati target e stati di partenza
• la realtà transisce da uno stato all’astro tramite azioni
  • le azioni hanno effetto deterministico
• il dominio della realtà é statico
• l’algoritmo di ricerca determina una soluzione
  • permette di raggiungere da uno stato iniziale uno stato target
    • una soluzione é un percorso del grafo degli stati
  • utilizza:
    • descrizione del problema
    • metodo di ricerca

Fornendo una situazione iniziale e una situazione da raggiungere, appartenenti allo stesso dominio, l’agente deve trovare una soluzione

Problemi

Un problema può essere definito formalmente come una tupla di 4 elementi

1. Stato iniziale
2. Funzione successore
3. Test Obiettivo
4. Funzione del costo del cammino

Aspirapolvere

Gioco del 15

Problema di ricerca nello spazio degli stati

• stato iniziale, qualsiasi
• funzione successore, spostamento di una tessera adiacente allo spazio vuoto nel suddetto
• test obiettivo, verifica che la stato sia quello desiderato (tabella ordinata)
• costo del cammino, ogni passo costa 1 e il costo del cammino é il numero di passi che lo costituiscono

• Euristiche

  • \(h_1\) numero delle tessere fuori posto (rispetto alla configurazione goal)
  • \(h_2\) distanza di Manhattan
    • in particolare \[\sum_{\forall c}d_{\text{man}}( c)\]

8 Regine

Posizionare 8 regine su una scacchiera \(8\times8\) in modo che nessuna sia sotto attacco

• generalizzabile con \(N\) regine su una scacchiera \(N\times N\)

Spazio degli Stati

Le caratteristiche di questi problemi sono:

• stati discreti
• effetto deterministico delle azioni
• dominio statico

Ricerca non informata - Blind

Costruiscono strutture dati proprie utilizzate nella soluzione di un problema

• alberi o grafi di ricerca
  • in un albero uno stato può comparire più volte

Ogni nodo rappresenta uno stato, una soluzione é un particolare percorso dalla radice ad una foglia

• i nodi figli sono creati dalla funzione successore
  • questi sono creati mantenendo un puntatore al padre, in modo da risalire una volta individuata la soluzione

Gli approcci sono valutati secondo

• completezza, garanzia di trovare una soluzione se esiste
• ottimalità, garanzia di trovare una soluzione ottima¹
• complessità temporale, tempo necessario per trovare una soluzione
• complessità spaziale, spazio necessario per effettuare la ricerca

NB \(\quad\) Lo studio della Complessità di un algoritmo é trattato anche in Algoritmi e Strutture Dati e Calcolabilità e Complessità.

Gli alberi vengono esplorati tramite Ricerca in Ampiezza e Ricerca in Profondità

Nello studio di queste ricerche si considerano:

• \(d\) profondità minima del goal
• \(b\) branching factor

Un goal a meno passi dalla radice non dà garanzia di ottimalità, in quanto vanno considerati i costi non il numero di passi. Il costo per l’ottimalità é una funzione monotona crescente in relazione alla profondità.

• Ricerca in Ampiezza

  • completa a patto che \(b,d\) siano finiti
  • ottima solo se il costo del cammino é \(f\) monotona crescente della profondità

  \[\textsc{time} = \textsc{space} = O(b^{d+1})\]

  • esponenziale, non trattabile anche con \(d\) ragionevoli

• Ricerca Costo Uniforme

  Cerca una soluzione ottima, che non in tutti i problemi corrisponde al minor numero di passi. La scoperta di un goal non porta alla terminazione della ricerca. Questa termina solo quando non possono esserci nodi non ancora scoperti con un costo minore di quello già trovato.

  La ricerca può non terminare in caso di no-op, che creano loop o percorsi infiniti sempre allo stesso stato. Quindi: \(\text{costi} \ge \epsilon > 0\)

  • \(\epsilon\) costo minimo
  • condizione necessaria per garantire ottimalità e completezza

  \[\textsc{time} = \textsc{space} = O(b^{1+\lfloor \frac{C^{*}}{\epsilon} \rfloor})\]

  • \(C^{*}\) costo soluzione ottima

• Ricerca in Profondità w/o Backtracking

  Si esplora espandendo tutti i figli ogni volta che viene visitato un nodo non goal

  • viene utilizzato uno stack (LIFO) per gestire la frontiera

  \[\textsc{time} = O(b^{m})\] \[\textsc{space} = O(b \cdot m)\]

• Ricerca in Profondità w/ Backtracking

  Si producono successori su successori man mano, percorrendo in profondità l’albero. In fondo, in assenza di goal, viene fatto backtracking cercando altri successori degli nodi già percorsi.

  • viene esplorato un ramo alla volta, in memoria rimane solo il ramo che sta venendo esplorato
  • più efficiente in utilizzo della memoria

  \[\textsc{time} = O(b^{m})\] \[\textsc{space} = O(m)\]

• Iterative Deepening

  Ricerca a profondità limitata in cui questa viene incrementata a ogni iterazione

  • ogni iterazione viene ricostruito l’albero di ricerca
  • cerca di combinare ricerca in profondità e in ampiezza
    • completa con \(b\) finito
    • ottima quando il costo non é funzione decrescente delle profondità

  \[\textsc{time}= O(b^d)\] \[\textsc{space}= O(b\cdot d)\]

• Ricerca Bidirezionale

  2 ricerche parallele

  • forward dallo stato iniziale
  • backwards dallo stato obiettivo

  Termina quando queste si incontrano a una intersezione. Il rischio é che si faccia il doppio del lavoro e che non convergano a metà percorso ma agli estremi

  • \(\textsc{time}= O( b^{\frac{d}{2}})\)
    • nel caso in cui le due ricerche si incontrino a metà

Ricerca informata

Si possiedono informazioni che permettono di identificare le strade più promettenti

• in funzione del costo

Questa informazione é chiamata euristica

• \(h(n)\): Il costo minimo stimato per raggiungere un nodo goal da \(n\)

Una strategia é il mantenere la frontiera ordinata secondo una \(f(n)\) detta funzione di valutazione

• questa contiene a sua volta una componente \(h(n)\) spesso
• in generale questa strategia é chiamata best-first search, il nodo più promettente é espanso per primo
  • si tratta di una famiglia di strategie (greedy, A*, RBFS)

• Greedy

  • costruisce un albero di ricerca
  • mantiene ordinata la frontiera a seconda di \(h(n)\)
    • \(f(n) = h(n)\)

  Ma l’euristica può essere imperfetta e creare dei problemi. Questa strategia considera solo informazioni future, che riguardano ciò che non é ancora stato esplorato.

• A*

  Combina informazioni future e passate:

  • Greedy e Ricerca a costo uniforme

  Utilizza una funzione di valutazione: \(f(n) = g(n) + h(n)\)

  • \(g(n)\) é il costo minimo dei percorsi esplorati che portano dalla radice a \(n\)

  I costi minimi reali sono definiti con: \(f^{\star}(n) = g^\star(n) + h^\star(n)\)

  • definizione utilizzata nelle dimostrazioni

  \(A^\star\) é ottimo quando

  • tutti i costi da un nodo a un successore sono positivi
  • l’euristica \(h(n)\) é ammissibile

  Ammissibilità

  • \(\forall n: h(n) \le h^\star(n)\)
    • ovvero l’euristica é ottimistica

  Nel caso di ricerca in grafi \(h(n)\) deve essere anche monotona consistente per garantire l’ottimalità.

  • vale una disuguaglianza triangolare
  • \(h(n) \le c(n,a,n') + h(n')\)
  • \(\textsc{nb}\) tutte le monotone sono ammissibili ma non vale il viceversa

  Inoltre é ottimamente efficiente e completo

  • espande sempre il numero minimo di nodi possibili

  Ma \(\textsc{space}=O(b^d)\)

  Algoritmo implementato in Python:

  # Code snippet found on rosettacode.org
  F AStarSearch(start, end, barriers)
     F heuristic(start, goal)
        V D = 1
        V D2 = 1
        V dx = abs(start[0] - goal[0])
        V dy = abs(start[1] - goal[1])
        R D * (dx + dy) + (D2 - 2 * D) * min(dx, dy)
  
     F get_vertex_neighbours(pos)
        [(Int, Int)] n
        L(dx, dy) [(1, 0), (-1, 0), (0, 1), (0, -1), (1, 1), (-1, 1), (1, -1), (-1, -1)]
           V x2 = pos[0] + dx
           V y2 = pos[1] + dy
           I x2 < 0 | x2 > 7 | y2 < 0 | y2 > 7
              L.continue
           n.append((x2, y2))
        R n
  
     F move_cost(a, b)
        L(barrier) @barriers
           I b C barrier
              R 100
        R 1
  
     [(Int, Int) = Int] G
     [(Int, Int) = Int] f
  
     G[start] = 0
     f[start] = heuristic(start, end)
  
     Set[(Int, Int)] closedVertices
     V openVertices = Set([start])
     [(Int, Int) = (Int, Int)] cameFrom
  
     L openVertices.len > 0
        (Int, Int)? current
        V currentFscore = 0
        L(pos) openVertices
           I current == N | f[pos] < currentFscore
              currentFscore = f[pos]
              current = pos
  
        I current == end
           V path = [current]
           L current C cameFrom
              current = cameFrom[current]
              path.append(current)
           path.reverse()
           R (path, f[end])
  
        openVertices.remove(current)
        closedVertices.add(current)
  
        L(neighbour) get_vertex_neighbours(current)
           I neighbour C closedVertices
              L.continue
           V candidateG = G[current] + move_cost(current, neighbour)
  
           I neighbour !C openVertices
              openVertices.add(neighbour)
           E I candidateG >= G[neighbour]
              L.continue
  
           cameFrom[neighbour] = current
           G[neighbour] = candidateG
           V H = heuristic(neighbour, end)
           f[neighbour] = G[neighbour] + H
  
     X RuntimeError(‘A* failed to find a solution’)
  

  Code Snippet 1: a-star.py

• Recursive Best-First Strategy

  RBFS

  • simile alla ricerca ricorsiva in profondità
  • usa un upper bound dinamico
    • ricorda la migliore alternativa fra i percorsi aperti
  • ha poche esigenze di spazio
    • mantiene solo nodi del percorso corrente e fratelli, in questo é migliore di A*
  • lo stesso nodo può essere visitato più volte se l’algoritmo ritorna a un percorso aperto

  Intuitivamente:

  • procede come \(A^{\star}\) fino a che la soluzione rispetta l'upper bound
  • sospende la ricerca lungo il cammino quando non più migliore
    • il cammino viene dimenticato, si cancella dalla memoria
    • é conservata la traccia nella sua radice del costo ultimo stimato

  L’algoritmo ha 3 argomenti

  • \(N\) nodo
  • \(f(N)\) valore
  • \(b\) upper bound
    • inizialmente impostato a \(+ \infty\)

  RBFS é ottimo se l’euristica é ammissibile \[\textsc{Space} = O(b\cdot d)\] \(\textsc{Time}\) dipende dall’accuratezza dell’euristica.

Euristiche

La qualità di un euristica può essere calcolata computando il branching factor effettivo \(b^\star\)

• \(N\) numero di nodi generati a partire da un nodo iniziale
• \(d\) profondità della soluzione trovata

\[N+1 = 1 + b^\star + (b^\star)^{2} + \cdots + (b^\star)^{d} \] \[N \simeq (b^\star)^{d} \implies b^\star \simeq \sqrt[d]{N}\]

Le euristiche migliori mostreranno \(b^\star\) vicini a 1.

Calcolo della Bontà

Per decidere tra 2 euristiche ammissibili quale sia la più buona

1. confronto sperimentale
2. confronto matematico

Si considera la dominanza

• \(\forall n : h_2(n) \le h_1(n)\le h^\star(n)\)
  • \(h_{1}\) domina perché restituisce sempre valore maggiore rispetto all’altra
  • si può dire sia più informata in quanto approssima meglio \(h^{\star}\)
• una euristica dominante Sara più vicina alla realtà

Si può costruire una nuova \(h(n) = \max(h_1(n),\dots,h_k(n))\) dominante su tutte quelle che la compongono

Si valuta la qualità dell’euristica (sperimentalmente) con il branching factor effettivo \(b^\star\)

• si costruisce con gli \(N\) nodi costruiti nella ricerca un albero uniforme
• \(b^\star\) piccolo \(\rightarrow\) euristica efficiente

Ricerca in Spazi con Avversari

Informazione può essere caratterizzata da:

• condizioni di scelta a informazione
  • perfetta
  • imperfetta
• effetti della scelta
  • deterministici
  • stocastici

La ricerca in questo ambito si basa su delle strategie basate su punteggi dati dagli eventi. In questo ambito si studiano spesso giochi.

I giochi non vengono scelti perché sono chiari e semplici, ma perché ci danno la massima complessità con le minime strutture iniziali. \(\qquad\qquad\qquad\) Marvin Minsky #cit

Alcuni giochi sono anche a somma zero se le interazioni tra gli agenti se portano a una perdita/guadagno per uno ciò compensato da un guadagno/perdita dell’altro, suo avversario. I nodi terminali dei grafi creati nella risoluzione di questi giochi posso indicare stati di vittoria, sconfitta, parità.

Teoria delle Decisioni

Dall’Economia, poi traslata in algoritmi nell’ambito dell’IA.

• approccio maximax - ottimistico
• approccio maximin - conservativo
• approccio minimax regret - minor regret
  • best payoff - real payoff

L'osservabilità é totale nei giochi a turno e parziale nei giochi ad azione simultanea. I giocatori Min e Max tengono conto dell’avversario nel calcolo dell’utilità degli stati

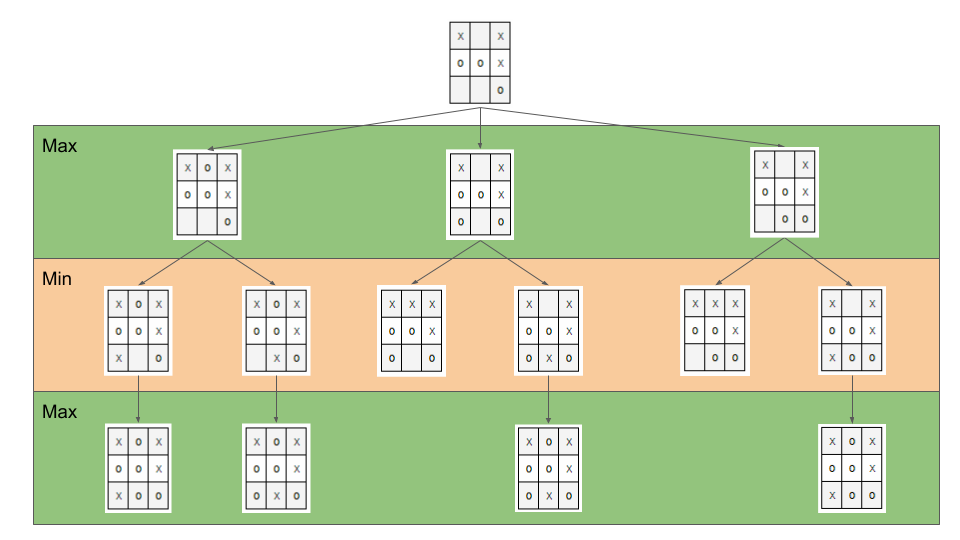
• Minimax

  Minimax é un algoritmo pessimista nel senso che simula che Min si muova in modo perfetto.

  • ricerca in profondità, esplora tutto l’albero ma non mantiene tutto in memoria

  Nella simulazione dell’albero di gioco si hanno i due attori

  1. Max
  2. Min

  L’algoritmo fa venire a galla i costi terminali dei rami del gioco, in quanto per guidare la scelta Max deve poter scegliere tra i nodi a se successivi.

  • é completo in grafi finiti
  • é ottimale se Max e Min giocano ottimamente

  La funzione utilità valuta gli stati terminali del gioco, agisce per casi sul nodo \(n\) in maniera ricorsiva \(\text{minimax-value}(n)\):

  • se \(n\) terminale
    • \(\text{utility}(n)\)
  • se \(n\) Max
    • \(\text{max}_{s \in succ(n)}(\text{minimax-value}(n))\)
  • se \(n\) Min
    • \(\text{min}_{s \in succ(n)}(\text{minimax-value}(n))\)

  def minimaxDecision(state): # returns action
      v = maxValue(state)
      return action in succ(state) with value == v
  
  def maxValue(state): # returns utility-value (state)
      if (state.isTerminal()):
          return utility(state)
  
      v = sys.minint
      for (a,s) in succ(state): # (action,successor)
          v = max(v, minValue(s))
  
      return v
  
  def minValue(state):
      if (state.isTerminal()):
          return utility(state)
  
      v = sys.maxint
      for (a,s) in succ(state):
          v = min(v, maxValue(s))
  
      return v
  

  \[\textsc{Space} = O(b \cdot m)\] \[\textsc{Time} = O(b^{m})\]

  • Potatura alpha-beta

    • Handout MIT sull’argomento per approfondire

    Per migliorare la complessità temporale dell’algoritmo si agisce potando le alternative che non potranno cambiare la stima corrente a quel livello. La potatura viene fatta in base all’intervallo \(\alpha \cdots \beta\) dove:

    • \(\alpha\) é il valore della migliore alternativa per Max nel percorso verso state
    • \(\beta\) é il valore della migliore alternativa per Min nel percorso verso state

    Se il \(v\) considerato é fuori da questo intervallo allora é inutile considerarlo.

    def alphabetaSearch(state): # returns action
        v = maxValue(state, sys.minint, sys.maxint)
        return action in succ(state) with value == v
    
    def maxValue(state, alpha, beta): # returns utility-value (state)
        if (state.isTerminal()):
            return utility(state)
    
        v = sys.minint
        for (a,s) in succ(state): # (action,successor)
            v = max(v, minValue(s, alpha, beta))
            if (v >= beta) return v
            alpha = max(alpha, v)
    
        return v
    
    def minValue(state, alpha, beta):
        if (state.isTerminal()):
            return utility(state)
    
        v = sys.maxint
        for (a,s) in succ(state):
            v = min(v, maxValue(s, alpha, beta))
            if (v <= alpha) return v
            beta = min(beta, v)
    
        return v
    

    Questo algoritmo é dipendente dall’ordine di esplorazione dei nodi, alcune azioni killer move permettono di tagliare l’albero subito e non sprecare passi.

    • \(\textsc{time} = O(b^{m/2})\)
      • nel caso migliore
      • se l’ordine é sfavorevole é possibile che non avvengano potature
      • comunque molto costoso

    Esistono tecniche di apprendimento per le killer move, il sistema si ricorda le killer move passate e le cerca nelle successive applicazioni. Queste tecniche sono studiate in quanto la complessità continua a essere troppo alta per applicazioni RealTime:

    • trasposizioni
      • permutazioni dello stesso insieme di mosse
      • mosse che portano allo stesso stato risultante
      • vanno identificate ed evitate
    • classificazione stati di gioco
      • per motivi di tempo vanno valutati come foglie nodi intermedi a un certo cutoff
      • va valutata una situazione intermedia (orizzonte)
        • valutazione rispetto alla facilità di raggiungere una vittoria
        • attraverso un classificatore sviluppato in precedenza
    • quiescenza dei nodi, concerne la permanenza della negatività o positività della valutazione
      • se mantiene la propria valutazione bene nei continuo
      • non ribalta la valutazione nel giro di poche mosse

Constraint Satisfaction Problems

CSP

• serie di variabili di dati domini
• vincoli, condizioni
  • é soddisfatto con una dato assegnamento che per essere una soluzione deve essere
    1. completo, tutte le variabili sono assegnate
    2. consistente, tutti i vincoli sono rispettati

I problemi sono affrontati con approcci diversi in base alle caratteristiche del dominio (valori booleani/discreti/continui)

Algoritmi

• Generate and Test

  Bruteforce

  1. genera un assegnamento completo
  2. controlla se é una soluzione
  3. se si return altrimenti continue

  É estremamente semplice ma non é scalabile.

• Profondità con Backtracking

  Si esplora l’albero delle possibili assegnazioni in profondità. Si fa backtracking quando si incontra una assegnazione parziale che non soddisfa più le condizioni. Il problema é che in CSP il branching factor é spesso molto alto, producendo alberi molto larghi.

  Dati \(n\) variabili e \(d\) media del numero di valori possibili per una variabile:

  • il branching factor al primo livello, \(n \cdot d\)
  • … al secondo, \((n-1)\cdot d\)
  • l’albero avrà \(n! \cdot d^{n}\) foglie

  Questo é migliorabile con la tecnica del fuoco su una singola variabile a ogni livello dell’albero, questo in quanto i CSP godono della proprietà commutativa rispetta all’ordine delle variabili. Questo permette di rimuove il fattoriale nel numero di foglie.

  Uno dei difetti di questo approccio é il Thrashing, riconsiderando assegnamenti successivi che si sono già dimostrati fallimentari durante l’esplorazione.

• Forward Checking

  Approccio locale di propagazione della conoscenza. Si propagano le scelte delle variabili ai vicini diretti, restringendo il dominio di questi vicini. In caso di individuare una inconsistenza se esiste.

• AC-3

  Arc Consistency - McWorth

  • funziona con vincoli binari
  • simile al Forward Checking
  • Arc Consistency non é una proprietà sufficiente a garantire l’esistenza di una soluzione

  def AC-3(csp): # returns redox CSP
      queue = csp.arcs
      while queue != empty:
          (xi,xj) = queue.RemoveFirst()
          if (RemoveInconsistentValues(xi,xj)):
              for (xk in xi.neighbours):
                  queue.Add(xk,xi)
  
  
  def RemoveInconsistentValues(xi,xj): # returns boolean
      removed = false
      for (x in Domain[xi])
          if (no value y in Domain[xj] consents to satisfy the constraint xi,xj):
              Domain[xi].delete(x)
              removed = true
      return removed
  

• Back-Jumping

  Risolve i limiti del tradizionale Backtracking Cronologico, che torna passo per passo indietro senza sfruttare i vincoli. Si viene guidati dal Conflict Set. Si fa backtracking a una variabile che potrebbe risolvere il conflitto.

  • questi CS sono costruiti tramite Forward Checking durante gli assegnamenti

  Sia \(A\) un assegnamento parziale consistente, sia \(X\) una variabile non ancora assegnata. Se l’assegnamento \(A \cup \{X=v_{i}\}\) risulta inconsistente per qualsiasi valore \(v_{i}\) appartenente al dominio di \(X\) si dice che \(A\) é un conflict set di \(X\)

  Quando tutti gli assegnamenti possibili successivi a \(X_{j}\) falliscono si agisce con il Back-Jumping

  • si considera l’ultimo assegnamento \(X_{i}\) aggiunto al CS di \(X_{j}\)
  • viene aggiornato il CS di \(X_{i}\)
    • \(CS(X_{i})=CS(X_{i})\cup (CS(X_{j})- \{X_{i}\})\)

Euristiche

• di variabile
  • Minimum Remaining Values - fail-first
  • Grado
• di valore
  • Valore Meno Vincolante
    • lascia più libertà alle variabili adiacenti sul grafo dei vincoli

Euristiche di scelta e inferenza

• alternanza tra esplorazione e inferenza
  • ovvero propagazione di informazione attraverso i vincoli

• Consistency

  1. Node Consistency
     • vincoli di arità 1 soddisfatti
  2. Arc Consistency
     • vincoli di arità 2 soddisfatti per ogni valore nel dominio
     • un arco é arc-consistent quando \(\forall\) valore del dominio del sorgente \(\exists\) valore nel dominio della destinazione che permetta di rispettare il vincolo
  3. Path Consistency
     • 3 variabili legate da vincoli binari
     • considerate 2 variabili \(x, y\) queste sono path-consistent con \(z\) se \(\forall\) assegnamento consistente di \(x,y \; \exists\) un assegnamento \(z\) tale che \(\{x,z\}\) e \(\{y,z\}\) questi sono entrambi consistenti.

  Questi concetti sono generalizzabili con la k-consistenza

  • per ogni sottoinsieme di \(k-1\) variabili e per ogni loro assegnamento consistente é possibile identificare un assegnamento per la \(k\text{-esima}\) variabile che é consistente con tutti gli altri.

  Un CSP fortemente consistente (k-consistente per \(k\) e tutti i \(k_{i}\) minori di \(k\)) puó essere risolto in tempo lineare.

Vincoli Speciali

• AllDifferent
  • test sul numero di valori rimanenti nei domini delle variabili considerate
• Atmost
  • disponibilitá \(N\)
  • risorse richieste dalle entitá
  • vincoli utilizzati nella logistica

Problema dell’Australia

3 colori per colorare i 7 territori dell’Australia

• {NA, NT, SA, Q, NSW, V, T}
• un territorio deve avere colore diverso da tutti i confinanti

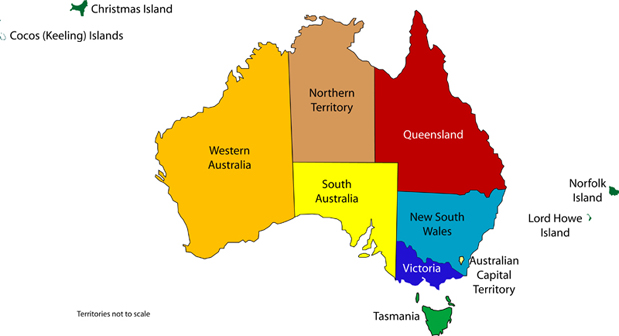
Rappresentazione della Conoscenza

Agenti su Conoscenza

Caratterizzati da:

• Knowledge Base
  • generalmente cambia nel tempo
  • inizialmente formata dalla background knowledge
• Tell - assert
• Ask - query
  • ogni risposta deve essere una conseguenza di asserts e background knowledge

Formalismi Logici

Per la rappresentazione di Knowledge Base

• Linguaggio di Rappresentazione
  • con cui vengono formate formule ben formate
  • la semantica del linguaggio definisce la veritá delle formule
• Modello \(F_n\)
  • é un assegnamento di valori ai simboli proposizionali
  • permette la valutazione delle formule
• Conseguenza \(\vDash\)
  • in generale il lato sinistro é sottoinsieme del destro
    • per ogni caso di \(F_{1}\) vale anche \(F_{2}: F_{1} \vDash F_{2}\)
  • non é l'implicazione logica, sono su piani diversi anche se sono simili
• Equivalenza \(\equiv\)
  • \(F_{1} \vDash F_{2} \land F_{2} \vDash F_{1}\)
• Validitá
  • o tautologia
  • vera in tutti i modelli
• Insoddisfacibilità
  • o contraddizione
  • una formula ins. é falsa in tutti i modelli
• Soddisfacibilità
  • formula per il quale esiste qualche modello in cui é vera
• Inferenza \(\vdash\)
  • propagazione informazione

\[\frac{\text{premesse}}{\text{conclusione}}\]

• Algoritmi di Inferenza manipolano inferenze per derivare formule
  1. correttezza (soundness)

\[KB \vdash_{i} A \implies KB \vDash A\]

1. completezza

\[KB \vDash_{} A \implies KB \vdash_{i} A\]

• Grounding

Semantica

\[KB_{LP}\vDash P_{LP}\]

Vari approcci:

1. Model Checking
   • \(n\) simboli, \(2^{n}\) modelli possibili
   • inefficiente
2. Theorem Proving
   • basato sull’inferenza sintattica
     • quindi sulla manipolazione delle formule
     • utilizza le Regole di Inferenza
       • contrapposizione, de Morgan, associatività…
   • Teorema di Deduzione
     • date formule \(R,Q\)
     • \(R\vDash Q \iff R\implies Q \text{ é una formula valida o tautologia}\)
       • \(Q\) é conseguenza logica di \(R\)

Theorem Proving

1. Algoritmo di Ricerca (o di inferenza)
2. Insieme di regole di inferenza
   • Risoluzione
     • disgiunzioni in cui si fattorizzano analoghi e si cancellano i contrari
     • il Modus Ponens ne é un caso particolare
     • si applica a CNF
       • \(KB_{\text{LP}} \vdash KB_{\text{CNF}}\)
         1. si eliminano le biimplicazioni
         2. si eliminano le implicazioni
         3. si portano all’interno i not applicando de Morgan
         4. si eliminano le doppie negazioni
         5. si distribuisce or sull'and
       • congiunzioni di clausole (disgiunzioni di letterali)

Teorema: Se un insieme di clausole é insoddisfacibile la chiusura della risoluzione contiene la clausola vuota

Questo é utilizzato nella dimostrazione per refutazione.

• Horn Clauses

  Un caso particolare delle clausole.

  Una clausola di horn é una disgiunzione di letterali in cui al piú uno é positivo.

  ad esempio:

  \[\frac{\lnot A \lor \lnot B \lor C}{A \land B \Rightarrow C}\]

  \[\frac{\lnot A \lor \lnot B}{A \land B}\]

• Forward Chaining

  Va nell’ordine dell’inferenza

  • lineare nel numero di clausole
  • ogni clausola é applicata al più una volta
  • però sono applicate clausole inutili per il target

  

• Backward Chaining

  Parte dalla formula da dimostare e va a ritroso

  • piú efficiente del Forward Chaining
  • meno che lineare

  

First Order Logic

• dichiarativa
  • separa conoscenza da inferenza
  • si deriva conoscenza da altra conoscenza

Elementi:

• costanti
• predicati
• variabili
• funzioni
  • NB questi non costruiscono oggetti: danno un riferimento a oggetti esistenti
• connettivi
• ugualianza
• quantificatori
  • \(\forall\) viene espanso in una catena di \(\land\)
  • \(\exists\) viene espanso in una catena di \(\lor\)
  • le espansioni vengono fatte sostituendo alla variabile tutte le costanti del modello
  • \(\exists x \lnot F \equiv \lnot \forall x F\)
  • \(\exists x F \equiv \lnot \forall x \lnot F\)
• punteggiatura

Le formule in FOL sono poi interpretate

• l’interpretazione forma un mapping tra simboli e dominio
• collega simboli e significati
  • funzioni - relazioni
  • predicati - relazioni
  • costanti - oggetti

Un modello é una coppia: \(M = \langle D,I \rangle\)

• \(D\) dominio
• \(I\) interpretazione

Come nellla logica proposizionale, \(M\) é un modello per \(\alpha\) se questo é vero in \(M\).

I modelli di un insieme di formule del prim’ordine possono essere infiniti.² Un termine é ground quando non contiene variabili. (i.e. fondato)

La base di conoscenza puó essere interrogata con ask

• quando compare una formula ground é banale la richiesta
• quando compaiono variabili si intende una sostituzione
  • quindi la variabile \(x\) é interpretata in senso esistenziale ( \(\exists\) )

• Clausole di Horn

  • disgiunzioni di letterali di cui al piú uno é positivo
  • atomiche
  • implicazioni il cui antecedente é una congiunzione di letterali

• Inferenza su FOL

  • Proposizionalizzazione
    • \(KB_{\text{FOL}} \rightarrow KB_{\text{LP}}\)
    • Regola di Instanziazione Universale - UI
      • \(\frac{\forall x, \alpha}{\text{subst}\{\{x/g\},\alpha\}}\)
      • alla fine, in uno o piú passi, si deve arrivare a ground, \(g\) é esso stesso ground
      • la \(KB_{\text{LP}}\) risultante é logicamente equivalente a quella precedente
    • Regola di Instanziazione Esistenziale - EI
      • \(\frac{\exists x,\alpha}{\text{subst}\{\{x/k\},\alpha\}}\)
      • \(k\) costante di Skolem, nuova
        • non compare nella KB
      • la \(KB_{\text{LP}}\) risultante non é logicamente equivalente a quella precedente ma é soddisfacibile se \(KB_{\text{FOL}}\) lo é
    • Herbrand
      • se una formula é conseguenza logica della \(KB_{\text{FOL}}\), partendo dalla \(KB_{\text{LP}}\) ottenuta esiste una dimostrazione della sua veritá
        • \(KB \vDash F\)
      • se non é conseguenza logica … non é detto sia dimostrabile
        • \(KB \not\vDash F\) non sempre possibile
      • la logica del prim’ordine é semi-decidibile
    • Inefficienza
      • crea delle basi di conoscenza grandi con le regole
  • Lifting delle regole di inferenza
    • Regole di Inferenza \(\text{LP}\) trasformate in Regole di Inferenza \(\text{FOL}\)
    • Modus Ponens Generalizzato³

  \[\frac{p_{1}',\cdots ,p_{n}' \qquad p_{1} \land \cdots \land p_{n} \implies q}{\text{subst}(q,\Theta)}\]

  • \(\Theta\) é un unificatore di ciascuna coppia \(\langle p_{i}', p_{i} \rangle\) per cui \(p_{i}' \theta = p_{i} \theta\) per ogni \(i\in [1,n]\)
  • Unification (Martelli/Montanari)
    • algoritmo di ricerca che date due formule trova la sostituzione \(\theta\) piú generale che le unifichi
  • Forward Chaining
    • Corretto e Completo se la KB é una DATALOG⁴
      • in caso contrario il caso negativo puó non terminare
  • Backward Chaining
    • stesse considerazioni del FC ma piú efficiente
  • Lifting della Risoluzione⁵

  \begin{align*} \frac{l_{1}\lor \cdots \lor l_{k} \qquad m_{1} \lor \cdots \lor m_{n}}{\text{subst}(\Theta, l_{1} \lor \cdots \lor l_{i-1} \lor l_{i+1} \lor \cdots \lor l_{k} \lor m_{1} \lor \cdots \lor m_{j-1} \lor m_{j+1} \lor \cdots \lor m_{n})} \end{align*}

  • \(KB_{\text{FOL}} \rightarrow_{\text{traduzione}} KB_{\text{FOL-CNF}}\)
    1. Eliminazione delle implicazioni
    2. Spostamento delle negazioni all’interno (\(\lnot \forall \equiv \exists \lnot\))
    3. Standardizzazione delle variabili (rinomina variabili ambigue)
    4. Skolemizzazione (eliminazione degli \(\exists\))⁶
       • funzioni di Skolem in contesti \(\forall x_{1},x_{2},\cdots [\exists y P(y,x_{1},x_{2},\cdots)] \cdots [\exists z Q(z,x_{1},x_{2}\cdots)]\)
       • \(\forall x P (F(x), x_{})\) dove \(F\) é una funzione di Skolem. con parametri tutti i parametri quantificati universalmente
       • Caso Particolare, in assenza di parametri la \(F\) non ha parametri: é una costante
    5. Eliminazione dei \(\forall\)

Database Semantics

• unicitá dei nomi
• closed-world assumption
  • ció che non é rappresentato é falso
  • questo é diverso dalle Ontologie OWL che assumono un mondo aperto
    • esiste il concetto di ignoto oltre al vero/falso
• domain closure

Riduce il numero di modelli a un numero finito.

Le ontologie a loro differenza possono avere istanze con ulteriori proprietá rispetto al concetto cui appartengono.

Ontologie

Le categorie vengono reificate, rese oggetti

• questi oggetti sono utilizzati al posto dei predicati utilizzati in FOL

Vengono aggiunti predicati:

• Member applicabile a istanze di oggetti e una categoria
  • true se l’istanza appartiene alla categoria
• IS-A applicabile a due categorie
  • vera se la prima é una sottocategoria della seconda

Con questi elementi si possono definire tassonomie

• insieme di regole di sottocategorie / sottoclassi

Le categorie di una tassonomia possono essere caratterizzate tramite la definizione di proprietà:

• Member(X, Pallone) \(\Rightarrow\) Sferico(X)
• le proprietá si ereditano dalle superclassi
• possono essere contraddette dalle proprietá delle sottoclassi

Le categorie:

• possono essere disgiunte se non hanno istanze in comune nelle proprie sottoclassi
  • Disjoint(S)
• costituiscono una decomposizione esaustiva rispetto a una \(C\) loro superclasse quando le istanze di \(C\) sono esattamente l’unione delle istanze di queste sottoclassi
  • ExhaustiveDec(S,C)
• costituiscono una partizione se valgono entrambe le precedenti
  • Partition(S,C)

Strutturalmente:

• Part-of(x,y)
• On-top(x,y)

L'ontologia é una forma piú generale delle tassonomie

• hanno forma di grafo e non di albero
• si struttura in
  • T-box
    • generale, concettualizzazione intensionale
    • quantificato universalmente
  • A-box
    • su istanze specifiche, estensionale
    • contiene fatti che devono essere coerenti con il contenuto della T-box

Relazioni tra Ontologie

Nello stesso dominio:

1. \(O_{1}\) e \(O_{2}\) sono identiche; sono due copie dello stesso file
2. \(O_{1}\) e \(O_{2}\) sono equivalenti; condividono vocabolario e proprietà ma sono espresse in linguaggi diversi⁷
3. \(O_{1}\) estende \(O_{2}\); vocabolari e proprietà di \(O_{2}\) sono preservati in \(O_{1}\) ma non viceversa
4. Weakly-Translatable
   • non si introducono inconsistenze
5. Strongly-Translatable
   • il vocabolario di Source é completamente mappabile in concetti di Dest
   • le proprietá di Source valgono in Dest
   • non c’é perdita di informazione
   • non si introducono inconsistenze
6. Approx-Translatable
   • Source é Weakly-Translatable in Dest
   • possono essere introdotte delle inconsistenze

Ontologia come agente

L'ontologia é la Knowledge Base, che tramite un motore inferenziale unisce l’ontologia e i fatti conosciuti per rispondere a delle interrogazioni. Queste possono essere poste da software esterni o utenti. Sono rappresentazione di concettualizzazioni

Un’ontologia puó essere interrogata in maniere diverse

1. istanza appartiene a categoria
2. istanza gode di proprietá
3. differenza fra categorie
4. identificazione di istanze

Esempi ontologie: Provenance, Semantic Web Utilizzate da: DBpedia, CreativeCommons, FOAF, Press Association, Linked (Open) Data

Data Interchange

RDF - Resource Description Framework

• Un linguaggio / modello di rappresentazione
• Base di linguaggi come OWL, SKOS, FOAF
• Rappresentato in XML

Triple soggetto, predicato, oggetto possono essere rappresentate in forma di grafo.

Knowledge Engineering

1. Identificazione dei concetti
   • elencare tutti i concetti riferiti nel DB di partenza
   • solitamento sostantivi
   • definire etichette e descrizioni
   • identificare in seguito le sottoclassi
2. Controllare se esistono ontologie giá definite online almeno parzialmente
   • allineamento delle ontologie necessario se non compatibili
   • matching di ontologie
   • la corrispondenza non sará mai perfetta
3. definire T-box
4. definire A-box

Strumenti:

• Protégé
• CEL, FaCT++

Situation Calculus

Sulla base della FOL contruisce:

• Azione
  • cambia lo stato del mondo
  • oggetti immateriali, rappresentate dalle funzioni
  • \(\text{Move}(O,P_{1},P_{2})\)
• Situazione
  • stato di cose, solitamente il prodotto di azioni
  • il tempo non é gestito esplicitamente perché rappresentato dal susseguirsi delle azioni
  • possiamo rappresentarle con funzioni \(\text{Do}(\text{seq-az}, S)\)
    • sequenza ottenuta applicando la sequenza di azioni nella situazione \(S\)
    • \(\text{Do}([\;\;], S) = S\)
    • \(\text{Do}([a | r], S) = \text{Do}(r, \text{Result}(a,S))\)
  • le rappresentazioni \(\text{Do}\) ci danno delle proiezioni, permettendoci di ragionare sugli effetti delle azioni senza modificare la situazione. Ragionando sugli effetti.
• Fluente
  • proprietá/predicato che puó cambiare nel tempo
  • \(P(A,B,S)\)
  • \(\text{Holds}(P(A,B),S)\)
    • formula + situation
• Predicato Atemporale
  • proprietá/predicato che non é influenzata dalle azioni

Assiomi della azioni

1. applicabilitá, proprietá che devono valere nella situazione di partenza
   • \(\forall \text{params},s: \text{Applicable}(\text{Action}(\text{params}),s) \iff \text{Precond}(\text{params},s)\)
2. effetto, proprietá che devono valere nella situazione di arrivo
   • la soluzione semplice di riportare solamente le modifiche dello stato da parte dell’azione
   • frame problem
3. frame
   • \(\forall \text{params},s,\text{vars}: \text{Fluent}(\text{vars},s) \land \text{params} \neq \text{vars} \implies \text{Fluent}(\text{vars}, \text{Result}(\text{Action}(\text{params}),s))\)
4. Assioma di Stato Successore
   • aggiunto per sostituire gli assiomi di frame
   • Azione Applicabile \(\implies\) =
     • (Fluente vero nella= \(s\) risultante \(\iff\) l'azione lo rendeva vero \(\lor\) era vero e l'azione non l'ha reso falso)

Anomalia di Sussman

Perseguimento di goal complessi

1. suddividere il goal in sottogoal
2. raggiungere i sottogoal sequenzialmente

Non tutti i goal possono essere risolti suddividendoli prima in subgoal e affrontandoli in maniera sequenziale.

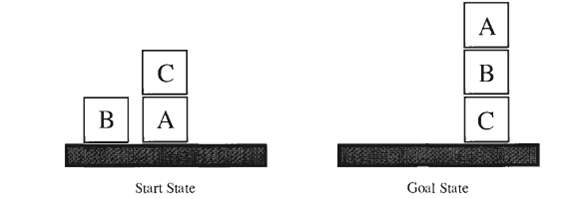
Agente

Ciclo di vita:

1. ha una percezione / ha un input
2. delibera / costruisce la risposta
3. agisce / restituisce la risposta

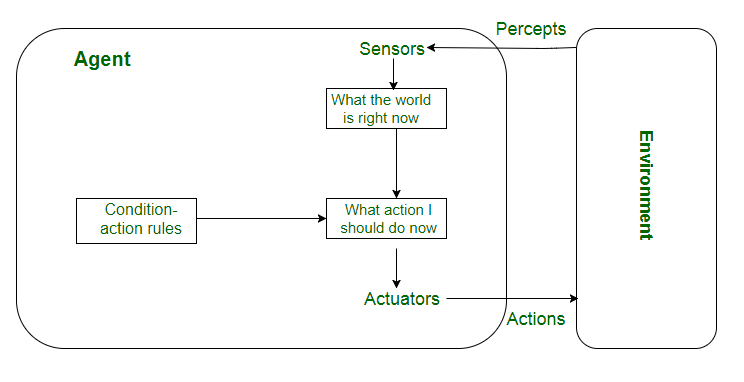
L'agente vive una sequenza percettiva, ovvero la storia completa delle percezioni

Deliberazione

Definibile come una \(f\) in forma tabellare

• sequenza percettiva | azione

Si misura la prestazione

• misura la bontá degli stati attraversati
• un’altra \(f\) che data una sequenza percettiva e valuta un valore di bontá

Queste considerazioni ci servono per definera la razionalitá del comportamento dell’agente.

• un agente razionale effettua azioni che lo avvicinano al proprio goal nei limiti dell’informazione a esso disponibile

Ambiente

• Task Environment
  • contesto in cui l’agente é inserito
  • fisico o meno
• PEAS, definiscono il Task Environment
  • performance
  • environment
  • actuators
  • sensors

Distinzione tra

• dinamico / statico
• monoagente / multiagente
  • in un sistema costituito da un insieme di agenti questi possono collaborare o competere nell’uso delle risorse e nel perseguimento dei propri obiettivi
  • va sviluppato un protocollo di interazione che permetta di coordinare piú agenti
    • attraverso scambi di messaggi
    • FIPA - Foundation for Intelligent Physical Agents
      • ha definito una semantica per i messaggi tra agenti e ha standardizzato dei protocolli

Architettura

Un'agente é l’unione di programma e architettura:

• architettura, specifica degli elementi strutturali e funzionali
• programma, funzione che mette in relazione percezioni e azioni

Si distingue anche tra:

• funzione agente, input la sequenza percettiva (storia delle percezioni)
• programma agente, input la percezione corrente

Tipologie:

• agenti reattivi semplici
  • reagisce alla percezione immediata
  • si basa sulla percezione corrente
  • funzionano in ambienti completamente osservabili
  • per evitare loop si introducono comportamenti random
• agenti reattivi basati su modello
  • agisce tramite modello - sequenza percettiva - storia delle azioni
  • mantiene uno stato
  • di base sempre un if - then
• agenti guidati dagli obiettivi - goal-driven
  • l’azione o piano di azione dell’agente é volto ad avvicinarlo all'obiettivo
  • cambiando gli obiettivi dell’agente posso fargli realizzare diversi comportamenti
• agenti guidati dall’utilitá - utility-driven
  • l’agente puó scegliere approcci diversi in base a parametri esterni
  • utilitá calcolabile
• agenti capaci di apprendere
  • la parte di apprendimento é caratterizzata da 3 elementi:
    • critico
      • valuta il livello di prestazione decidendo se attivare l’apprendimento
    • modulo dell’apprendimento
      • modifica la conoscenza dell’agente
    • generatore di problemi
      • causa l’esecuzione di azioni esplorative

Apprendimento Automatico

Molte tipologie diverse:

• classificatori a regole
• k-nearest neighbour
• classificatori bayesiani
• reti neurali
• support vector machines
• ensemble methods
• regressione

Classificazione

Dati \(\rightarrow f \rightarrow\) Classe

• questa \(f\) é il risultato dell’apprendimento

Tra i dati forniamo esempi ma anche le categorie. Costruisco un Learning Set costruito da coppie

• istanza \(x\) - classe \(y\)
  • le istanze sono tuple
• é supervisionato
• il rischio é che questo set di apprendimento sia troppo specialistico
  • non riconoscerá l’intera classe ma solamente una sua specializzazione

Con cui eseguo l'Apprendimento Supervisionato

• implementata tramite un algoritmo di apprendimento
• il modello viene costruito da questo
• il modello viene poi utilizzato per la predizione

Si pongono subito dei problemi:

1. rappresentazione dei dati/istanze
2. analisi dei dati
3. utilizzo della conoscenza costruita

Schema:

• Training Set \(\rightarrow\) Induzione \(\rightarrow\) Modello
• Test Set \(\rightarrow\) Deduzione \(\rightarrow\) Classe

I modelli si caratterizzano in:

• predittivi
  • strumento di previsione
  • assegna una appartenenza a istanze ignote
• descrittivi
  • strumento esplicativo
  • evidenzia caratteristiche che distinguono le categorie

Attributi

Gli attributi sono distinguibili in classi diverse

• binari
• nominali
  • assumono delle etichette distinte
  • definiti in un insieme
  • spit
    • multivalore
      • un nodo per ogni etichetta
    • binario
      • un nodo per una etichetta e uno per le rimanenti
• ordinali
  • sono nominali in cui vale una relazione di ordinamento tra le etichette
  • spit
    • multivalore
    • binario
      • possibile ma deve preservare l’ordinamento
• continui
  • si identifica un valore rispetto il quale fare split
    • in base a questo l’attributo diviene binario

Matrice di Confusione

É uno strumento di valutazione in ambito della classificazione. Consiste nel mettere alla prova il modello. Consiste in un insieme di istanze

• Test Set
• hanno la stessa forma del Learning Set
• il modello restituisce una classificazione di tutte le istanze
  • poi esaminate e suddivise in corrette e sbagliate
  • la percentuale desiderata di classificazioni corrette é relativo all’ambito, il dominio

La matrice di confusione é una matrice quadrata

• numero di righe/colonne come il numero delle classi
  • righe, classi reali
  • colonne, classi predette
  • il \(v\) in una cella \(\langle c_{i},c_{j} \rangle\)
    • numero di istanze appartenenti a \(c_{i}\) che il modello ha detto appartenere a \(c_{j}\)
    • desideriamo che i \(v\) si accumulino nella diagonale, dove troviamo le risposte corrette

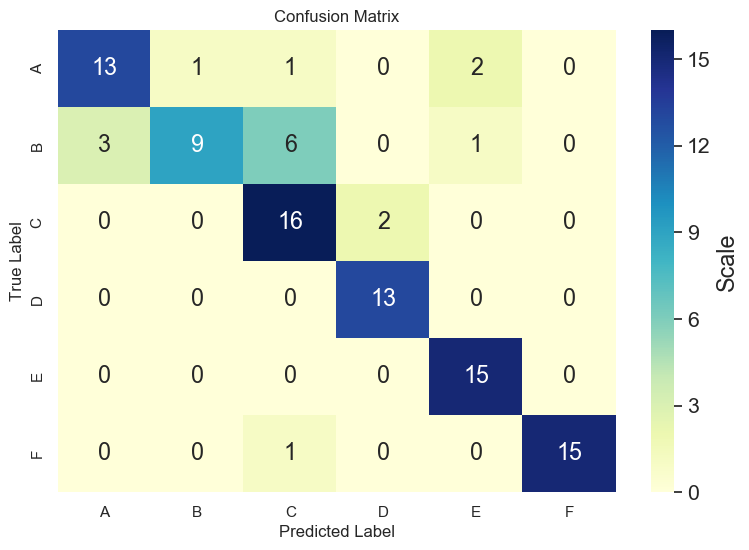
Si hanno due considerazioni sui risultati:

• accuracy

\[\frac{\sum_{i} v_{ii}}{\sum_{i,j} v_{ij}}\]

• error rate

\[\frac{\sum_{i \neq j} v_{ij}}{\sum_{i,j} v_{ij}}\]

Chiaramente \(\text{acc} + \text{er} = 100\%\)

Il limite della matrice di confusione é che gli errori hanno tutti lo stesso peso.

• per sopperire a questo si puó aggiungere una matrice dei costi
  • ha la stessa forma della matrice di confusione
  • gli errori saranno poi moltiplicati per questi pesi per valutare il modello

Altro limite é che su test set sbilanciati gli error rate saranno falsati.

Classificazioni a Regole

Si classifica secondo regole della forma

• antecedente
  • attributi, operazioni, valori
• conseguente
  • classe di appartenenza

Qualità di una regola valutata tramite

• copertura \(\frac{|A|}{|D|}\)
• accuratezza \(\frac{|A \cap y|}{|A|}\)

dove

• \(A\) istanze che soddisfano l’antecedente
• \(D\) dataset
• \(y\) sotto insieme di \(D\) di una particolare classe

Si desiderano

• regole mutualmente esclusive
  • attivate da insiemi di esempi disgiunti
  • se le regole non lo sono si utilizzano
    • liste di decisione
      • si decide in ordine di priorità
    • insiemi non ordinati
      • si decide secondo una votazione / conteggio
• regole esaustive
  • ogni possibile combinazione di valori degli attributi é catturata
  • se manca l’esaustività ciò implica che alcuni casi non saranno classificabili
    • in questi casi si definisce una classe di default

Le regole vengono ordinate secondo gli antecedenti o le classi.

Le regole sono prodotte

• indirettamente
  • estraendole da un albero di decisione
• direttamente
  • Sequential Covering

• Sequential Covering

  • focus su una classe alla volta, le altre sono considerate contro-esempi
  • ogni ciclo produce una regola
    • e vengono rimosse le istanze riconosciute da questa regola
    • Learn one Rule
      • general-to-specific
        • a partire dalla regola più generale \(\text{True}=y\)
        • si aggiungono all’antecedente in and delle specifiche, con le tecniche di scelta dello split
      • specific-to-general
        • scegliendo in modo casuale un esempio della classe definisce
        • valori dell’esempio
        • numero dei congiunti secondo gli attributi descritti dall’istanza
        • per generalizzare si eliminano dei congiunti utilizzando le tecniche di scelta dello split
  • le regole prodotte andranno poi utilizzate nell’ordine in cui sono prodotte

Valutazione

Il modello costruito é buono o no?

• se non lo é, qual’era il problema
  • parametri
  • algoritmo
  • classificatore
  • learning set

Ci sono diversi metodi di valutazione di un modello costruito tramite un algoritmo, é importante per la valutazione partendo da un dataset distinguere un learning e un test set nella maniera migliore possibile:

• Holdout
  • partizione dei dati disponibili in LS e TS
  • se la partizione è sbilanciata si va verso over o under fitting
• Random subsampling
  • si ripete il processo di holdout più volte
  • ripetendo più volte l’apprendimento
  • si fa una media delle valutazioni dei modelli generati
    • si valuta il classificatore in maniera più oggettiva
    • si cerca di liberare la valutazione dall’aleatorità dei partizionamenti
• Cross-validation
  • si fa random subsampling ma con dati più omogenei
  • \(K\) fold cross validation
    • con \(K\) partizioni
  • \(1\) dei set è usato come TS
  • \(K-1\) dei set sono accorpati in LS
  • uno per volta tutti i \(K\) set sono utilizzati per il testing
  • alla fine si fa una media delle valutazioni
• Bootstrap
  • in casi in cui il dataset é piccolo
  • per il LS si scelgono istanze dal dataset ma senza rimuoverle da quest’ultimo
    • una stessa istanza può apparire più volte nel LS
  • per il TS si scelgono le istanze con cui non si è fatto apprendimento
  • questo viene ripetuto e valutato a piacere, facendo la media

Tutte queste tecniche si usano nella valutazione dell’algoritmo usato rispetto al problema. In generale, per singoli modelli diversi costruiti con algoritmi diversi, non si puó contare sul fatto che i test siano stati fatti sugli stessi sotto-insieme di dati.

• nella valutazione quindi i risultati non possono che essere probabilistici
• si ottiene un'intervallo di confidenza
• altro parametro di una valutazione é il livello di confidenza

Split & Entropia

La scelta dello split viene effettuata considerando l’impatto o entropia

• generalmente, alberi compatti sono preferibili ad alberi con un numero di test maggiori
  • meno classi sono rappresentate in un nodo figlio meno confuso e' l’insieme e migliore e' lo split
• il Rasoio di Occam puo' essere utilizzato come criterio per la scelta
  • a parita' di assunzioni la spiegazione piu' semplice e' la preferita

Altri metodi di misura della bonta' di un split sono i Gini e Errori di classificazione.

Misure di selezione:

• \(p(i\mid t)\)
  • \(i\) classe
  • \(t\) insieme
  • probabilita' che l’elemento appartenga alla classe \(i\)

Si puo' calcolare una distribuzione di probabilita' di appartenenza di un record estratto casualmente. \[\text{Entropy}(t) = \sum_{i=0}^{c-1} - p(i \mid t) \log_{2}p(i\mid t)\]

• e' assunto che \(0 \log_{2} 0 = 0\)
• \(E=0\) e' il caso migliore, con distribuzioni \((0,1)\) o \((1,0)\)
• \(E=1\) e' il caso peggiore con distribuzione \((0.5,0.5)\)

Il calcolo della bonta' di uno split, o calcolo del guadagno \[\Delta = I(\text{parent}) - \sum_{j=1}^{k}\frac{N(v_{j})}{N} I(v_{j})\]

• \(I\) e' l’impurita'
• \(N\) numero record/istanze del nodo genitore
• \(N(v_{j})\) numero record/istanze del nodo figlio \(j\) -esimo

Nel caso della misura, utilizzando l’entropia si calcola l'information gain \[\Delta = E(\text{parent}) - \sum_{j=1}^{k}\frac{N(v_{j})}{N} E(v_{j})\]

Overfitting

Anche errore di generalizzazione.

Se il Learning Set manca di esempi oppure contiene noise, errori di classificazione, il modello generato puo' mancare di generalita'. Il modello ideale e' quello che produce il minor errore di generalizzazione possibile.

Il problema dell’overfitting si affronta diminuendo i test, rendendo meno specifico l’albero. Per questo si utilizzano tecniche di pruning, potatura.

• prepruning
  • si interrompe la costruzione del DT prima che sia completo
  • si ha una regola di terminazione restrittiva
    • non si esegue lo split se il gain é sotto una soglia
  • si può ricadere nel problema opposto del underfitting
• postpruning
  • lavora su albero costruiti completamente
  • con un insieme di dati supervisionati lo si analizza
    • i rami poco percorsi si rimuovono, si riducono a foglie
  • si spreca del lavoro fatto

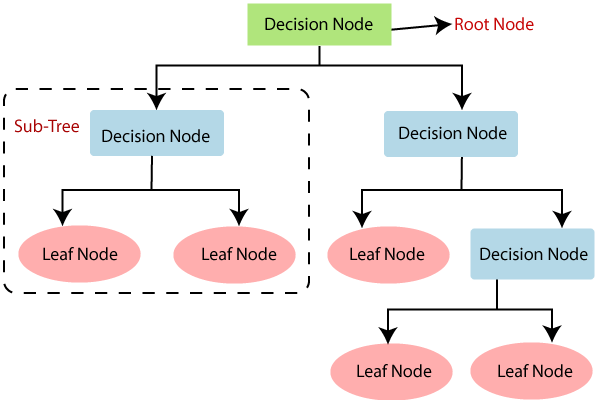
Alberi di Decisione

Decision Trees Banalmente, in un altro contesto, un menú a tendina.

• si tratta di un albero con test per nodi e azioni per foglie
  • test portano in base ai risultati a test successivi o foglie
  • alle foglie si decide la classe di appartenenza dell’istanza

Le istanze hanno la stessa forma

• n-attributi organizzati in una n-tupla

I test sono ognuno su un singolo attributo e a cascata caratterizzano le istanze.

Algoritmo di Hunt

L’algoritmo di Hunt lavora sul Learning Set

• dividendo in sottoinsiemi via via piú puri
• \(D_{t}\) sottoinsieme del LS associato al nodo \(t\)
• \(y = \{y_{1},y_{2},\cdots,y_{c}\}\) insieme delle etichette delle classi

Passi:

1. test se tutte le istanze in \(D_{t}\) appartengono alla stessa classe
   • true: \(t\) é una foglia e le viene assegnata l’etichetta \(y_{t}\)
   • false: si sceglie un attributo descrittivo su cui fare lo split
     1. si verifica il suo range in \(D_{t}\)
     2. si crea un nodo successore per ogni suo possibile valore
     3. a ogni successore si assegna il sottoinsieme di \(D_{t}\) per cui l’attributo scelto vale quello cui il successore é associato

Lazy Learning

Definition \(\quad\) Lazy Learning in machine learning is a learning method in which generalization beyond the training data is delayed until a query is made to the system, as opposed to in Eager Learning, where the system tries to generalize the training data before receiving queries. Lazy learning is essentially an instance-based learning: it simply stores training data (or only minor processing) and waits until it is given a test tuple.

Un lazy learner non costruisce un modello con i dati di apprendimento ed é di semplice implementazione. Un esempio di questi é K-NN.

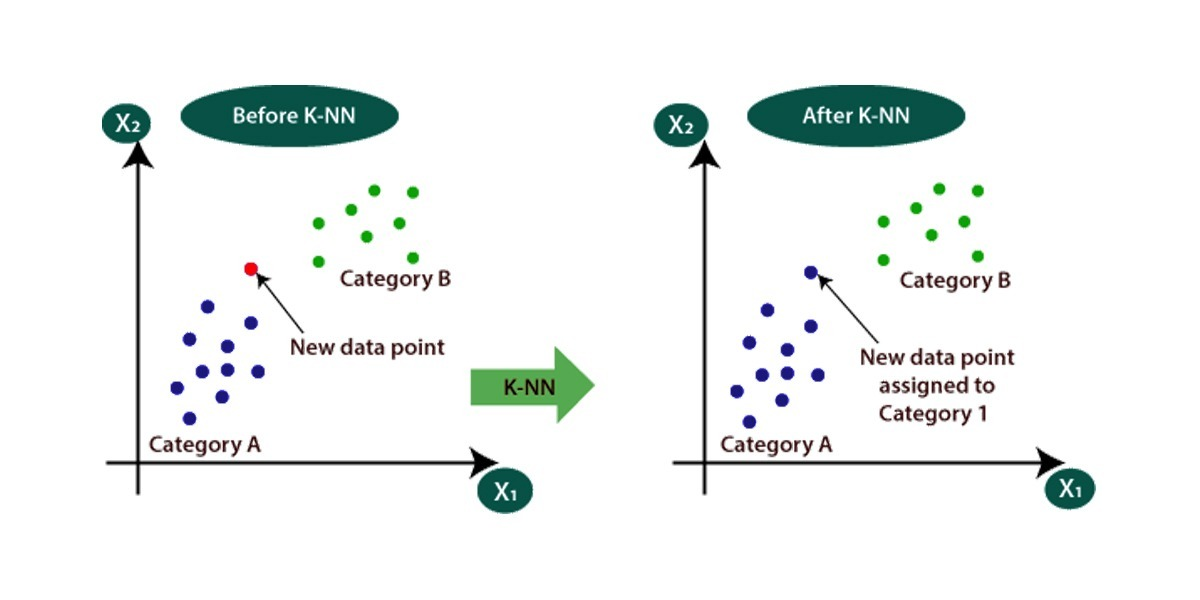
• k-Nearest Neighbours

Condividere caratteristiche é un’importante indicatore di una stessa classe di appartenenza.

• somiglianza \(\rightarrow\) stessa classe
  • a livello matematico significa vicinanza numerica
• le somiglianze sono trovate avendo memorizzato il LS

Si rappresentano come punti in uno spazio \($n\)-dimensionale le istanze: \[i = \langle v_{1}, v_{2}, \cdots , v_{n} \rangle\]

Questi punti vengono rapportati rispettivamente ai \(k\) punti piú vicini in funzione della loro distanza.

• un punto vicino a tutti punti di una stessa classe viene classificato/predetto come in quella classe
• in caso di discordanza della classe dei vicini ci sono diverse implementazioni
  • votazione, vince la maggioranza ma si perde l’informazione sulla distanza
  • votazione pesata, voti pesati rispetto alla distanza
• attributi di domini diversi possono avere cifre significative diverse
  • nella memorizzazione gli intervalli degli attributi vanno normalizzati
  • si effettuano le necessarie approssimazioni per creare una relazione tra distanza e similitudine

\[y = \text{argmax}_{v} \sum_{x_{i},y_{i}}^{k} \frac{I(v=y_{i})}{d(x', x_{i})^{2}}\] dove, ciclando su \(i\):

• \(x'\) dato da classificare
• \(y\) classe risultato
• \(y_{i}\) classe dell’istanza \(x_{i}\)
• \(x'\) \(n\)-tupla da classificare
• nominatore: somma dei voti per la classe \(y_{i}\)
• denominatore: divisione per peso calcolato sulla distanza

Neural Network

Perceptron

Prima proposta di modello di neurone artificiale

• ispirazione dalla biologia
• il piú semplice Neural Network possibile

Struttura:

• \(n\) input \(x_{i}\)
  • ciascuno con un peso \(w_{i}\)
  • formano una tupla di ingresso \(\langle x_{1},x_{2},\cdots ,x_{n} \rangle\)
• un output \(y\)
• memoria - unitá computazionale centrale
  • \(f(\text{net})\) funzione di attivazione con \(\theta\) soglia di attivazione.

\[\text{net} = \sum_{i=1}^{n} w_{i}x_{i}\] \[f(\text{net}) = \begin{cases}1 \quad \text{net}\ge \theta \\ 0 \quad \text{altrimenti} \end{cases}\]

Questa discontinuitá sulla soglia é stata sostituita successivamente da una sigmoide. \[f(\text{net}) = \frac{1}{1 + e ^{-\alpha(\text{net}- \theta)}}\]

Il percettrone codifica un test lineare. Delinea un iperpiano/iperspazio che divide lo spazio in due metá

• nelle vicinanze del confine la sigmoide transiziona da 1 a 0

L’apprendimento consiste nel trovare il taglio che divida le classi

• questo si fa apprendendo i pesi \(w_{i}\) necessari per la classificazione corretta
• tramite Learning Set supervisionato

\[w_{j}^{k+1} = w_{j}^{k} + \alpha (d - o) x_{j}\]

• \(\alpha \in [0,1]\) learning rate
• \(o\) output restituito per la tupla di input
• \(d\) output desiderato
• se \(o \neq d\) il percettore ha fatto un errore \(d-o\)

I \(w_{j}\) sono prodotti incrementalmente tramite questo processo e sono deposizione della conoscenza dell’apprendimento.

• l’apprendimento si ferma quando i cambiamenti ai pesi rallentano

• Limiti

  Rappresentazione dello XOR

  x	y	\(\oplus\)
  1	1	-
  1	0	+
  0	1	+
  0	0	-

  Non é risolvibile da un singolo perceptron, solo con tecniche piú sofisticate utilizzandone un altro.

Multilayer Perceptron

MLP

Si moltiplicano i perceptron posizionandoli in cascata e dividendoli per funzione

• output
  • \(n\) come le classi
  • questi neuroni danno output rispetto la class di appartenenza
• hidden
• input

I dati viaggiano in un’unica direzione e é pienamente connessa

• tutti i neuroni di un livello sono collegati a tutti quelli dello strato successivo

I livelli di percettori hidden possono identificare regioni dello spazio dei dati piú complesse

1. traccia confini
2. identifica forme chiuse
3. identifica regioni cave all’interno delle precedenti forme chiuse

• Epoca di Apprendimento

  • passata forward individua con le tuple del Learning Test l'errore
  • passata backward propaga l’informazione dell’errore a ritroso nella rete
    • aggiornando i pesi

  Si utilizza il metodo di apprendimento noto come Discesa del Grandiente. \[\Delta w_{ij} = - \lambda \frac{dE(\overline w)}{d w_{ij} }\]

  • \(E(\overline w)\) matrice dei pesi
  • si identifica la direzione in cui le configurazioni dei pesi si sviluppano rispetto all’errore
    • lo si abbassa minimizzando l’errore

  L’apprendimento nel MLP si puó sviluppare in 2 casi

  1. neurone di output \(o\) e neurone hidden \(i\) collegato direttamente a \(o\)
     • si calcola direttamente l’errore con la differenza
     • \(\Delta w_{ji} = \alpha \delta^{j} x_{ji}\) — variante di peso
     • \(\delta^{j} = y (1-y)(t-y)\) — viene distribuito sui predecessori
       • \(y (1-y)\) derivata \(f\) errore
       • \(t-y\) errore
  2. neurone dello strato hidden \(k\) a metá tra neuroni hidden o input \(i\) e altri hidden oppure output
     • propaghiamo verso \(i\)
     • \(\Delta w_{ki} = \alpha \delta^{k} x_{ki}\) — variante di peso
     • \(\delta^{k} = y (1-y) \sum_{j\in I} \delta^{j} w_{kj}\)
       • l’errore di questo livello dipende dall’errore fatto negli errori piú profondi
       • backpropagation o retropropagazione dell’errore